
ЁОЬтФПЁПФГЙЄГЇФГжжВњЦЗЕФФъЙЬЖЈГЩБОЮЊ250ЭђдЊЃЌУПЩњВњxЧЇМўЃЌашСэЭЖШыГЩБОЮЊCЃЈxЃЉЃЌЕБФъВњСПВЛзу80ЧЇМўЪБЃЌCЃЈxЃЉ= ![]() ЃЈЭђдЊЃЉЃЎЕБФъВњСПВЛаЁгк80ЧЇМўЪБЃЌCЃЈxЃЉ=51x+
ЃЈЭђдЊЃЉЃЎЕБФъВњСПВЛаЁгк80ЧЇМўЪБЃЌCЃЈxЃЉ=51x+ ![]() ЃЈЭђдЊЃЉЃЎУПМўЩЬЦЗЪлМлЮЊ0.05ЭђдЊЃЎЭЈЙ§ЪаГЁЗжЮіЃЌИУГЇЩњВњЕФЩЬЦЗФмШЋВПЪлЭъЃЎ
ЃЈЭђдЊЃЉЃЎУПМўЩЬЦЗЪлМлЮЊ0.05ЭђдЊЃЎЭЈЙ§ЪаГЁЗжЮіЃЌИУГЇЩњВњЕФЩЬЦЗФмШЋВПЪлЭъЃЎ
ЃЈ1ЃЉаДГіФъРћШѓLЃЈxЃЉЃЈЭђдЊЃЉЙигкФъВњСПxЃЈЧЇМўЃЉЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉФъВњСПЮЊЖрЩйЧЇМўЪБЃЌИУГЇдкетвЛЩЬЦЗЕФЩњВњжаЫљЛёРћШѓзюДѓЃП
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЁпУПМўЩЬЦЗЪлМлЮЊ0.05ЭђдЊЃЌ
ЁрxЧЇМўЩЬЦЗЯњЪлЖюЮЊ0.05ЁС1000xЭђдЊЃЌ
ЂйЕБ0ЃМxЃМ80ЪБЃЌИљОнФъРћШѓ=ЯњЪлЪеШыЉГЩБОЃЌ
ЁрLЃЈxЃЉ=ЃЈ0.05ЁС1000xЃЉЉ ![]() Љ10xЉ250=
Љ10xЉ250= ![]() +40xЉ250ЃЛ
+40xЉ250ЃЛ
ЂкЕБxЁн80ЪБЃЌИљОнФъРћШѓ=ЯњЪлЪеШыЉГЩБОЃЌ
ЁрLЃЈxЃЉ=ЃЈ0.05ЁС1000xЃЉЉ51xЉ ![]() +1450Љ250=1200ЉЃЈx+
+1450Љ250=1200ЉЃЈx+ ![]() ЃЉЃЎ
ЃЉЃЎ
злКЯЂйЂкПЩЕУЃЌLЃЈxЃЉ= 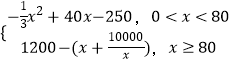
ЃЈ2ЃЉНтЃКгЩЃЈ1ЃЉПЩжЊЃЌ 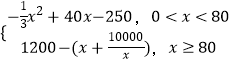 ЃЌ
ЃЌ
ЂйЕБ0ЃМxЃМ80ЪБЃЌLЃЈxЃЉ= ![]() +40xЉ250=Љ
+40xЉ250=Љ ![]() ЃЌ
ЃЌ
ЁрЕБx=60ЪБЃЌLЃЈxЃЉШЁЕУзюДѓжЕLЃЈ60ЃЉ=950ЭђдЊЃЛ
ЂкЕБxЁн80ЪБЃЌLЃЈxЃЉ=1200ЉЃЈx+ ![]() ЃЉЁм1200Љ2
ЃЉЁм1200Љ2 ![]() =1200Љ200=1000ЃЌ
=1200Љ200=1000ЃЌ
ЕБЧвНіЕБx= ![]() ЃЌМДx=100ЪБЃЌLЃЈxЃЉШЁЕУзюДѓжЕLЃЈ100ЃЉ=1000ЭђдЊЃЎ
ЃЌМДx=100ЪБЃЌLЃЈxЃЉШЁЕУзюДѓжЕLЃЈ100ЃЉ=1000ЭђдЊЃЎ
злКЯЂйЂкЃЌгЩгк950ЃМ1000ЃЌ
ЁрЕБВњСПЮЊ100ЧЇМўЪБЃЌИУГЇдкетвЛЩЬЦЗжаЫљЛёРћШѓзюДѓЃЌзюДѓРћШѓЮЊ1000ЭђдЊЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЗжСНжжЧщПіНјаабаОПЃЌЕБ0ЃМxЃМ80ЪБЃЌЭЖШыГЩБОЮЊCЃЈxЃЉ= ![]() ЃЈЭђдЊЃЉЃЌИљОнФъРћШѓ=ЯњЪлЪеШыЉГЩБОЃЌСаГіКЏЪ§ЙиЯЕЪНЃЌЕБxЁн80ЪБЃЌЭЖШыГЩБОЮЊCЃЈxЃЉ=51x+
ЃЈЭђдЊЃЉЃЌИљОнФъРћШѓ=ЯњЪлЪеШыЉГЩБОЃЌСаГіКЏЪ§ЙиЯЕЪНЃЌЕБxЁн80ЪБЃЌЭЖШыГЩБОЮЊCЃЈxЃЉ=51x+ ![]() ЃЌИљОнФъРћШѓ=ЯњЪлЪеШыЉГЩБОЃЌСаГіКЏЪ§ЙиЯЕЪНЃЌзюКѓаДГЩЗжЖЮКЏЪ§ЕФаЮЪНЃЌДгЖјЕУЕНД№АИЃЛЃЈ2ЃЉИљОнФъРћШѓЕФНтЮіЪНЃЌЗжЖЮбаОПКЏЪ§ЕФзюжЕЃЌЕБ0ЃМxЃМ80ЪБЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕЃЌЕБxЁн80ЪБЃЌРћгУЛљБОВЛЕШЪНЧѓзюжЕЃЌзюКѓБШНЯСНИізюжЕЃЌМДПЩЕУЕНД№АИЃЎ
ЃЌИљОнФъРћШѓ=ЯњЪлЪеШыЉГЩБОЃЌСаГіКЏЪ§ЙиЯЕЪНЃЌзюКѓаДГЩЗжЖЮКЏЪ§ЕФаЮЪНЃЌДгЖјЕУЕНД№АИЃЛЃЈ2ЃЉИљОнФъРћШѓЕФНтЮіЪНЃЌЗжЖЮбаОПКЏЪ§ЕФзюжЕЃЌЕБ0ЃМxЃМ80ЪБЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕЃЌЕБxЁн80ЪБЃЌРћгУЛљБОВЛЕШЪНЧѓзюжЕЃЌзюКѓБШНЯСНИізюжЕЃЌМДПЩЕУЕНД№АИЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФЕЅЕїдіЧјМфЃЛ
ЕФЕЅЕїдіЧјМфЃЛ
ЃЈ2ЃЉЩшКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЎШєКЏЪ§
ЃЎШєКЏЪ§![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєКЏЪ§![]() ЃЌ
ЃЌ ![]() ЕФЖЈвхгђЖМЪЧ
ЕФЖЈвхгђЖМЪЧ![]() ЃЌЖдгкКЏЪ§
ЃЌЖдгкКЏЪ§![]() ЕФЭМЯѓЩЯЕФШЮвтвЛЕу
ЕФЭМЯѓЩЯЕФШЮвтвЛЕу![]() ЃЌдкКЏЪ§
ЃЌдкКЏЪ§![]() ЕФЭМЯѓЩЯЖМДцдквЛЕу
ЕФЭМЯѓЩЯЖМДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЌ
ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЌ ![]() ЮЊзјБъдЕуЃЎЧѓ
ЮЊзјБъдЕуЃЎЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФВЛЕШЪНx2Љ2axЉ8a2ЃМ0ЃЈaЃО0ЃЉЕФНтМЏЮЊЃЈx1 ЃЌ x2ЃЉЃЌЧвЃКx2Љx1=15ЃЌдђa=ЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧњЯпy=1+ ![]() гыжБЯпy=kЃЈxЉ2ЃЉ+4гаСНИіНЛЕуЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
гыжБЯпy=kЃЈxЉ2ЃЉ+4гаСНИіНЛЕуЃЌдђЪЕЪ§kЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЫФИіУќЬтЃК
ЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂкШє![]() ЪЧВЛЙВЯпЕФЫФЕуЃЌдђ
ЪЧВЛЙВЯпЕФЫФЕуЃЌдђ![]() ЪЧЫФБпаЮ
ЪЧЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЕФГфвЊЬѕМўЃЛ
ЮЊЦНааЫФБпаЮЕФГфвЊЬѕМўЃЛ
ЂлШє![]() ЃЌ
ЃЌ ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
Ђм![]() ЕФГфвЊЬѕМўЪЧ
ЕФГфвЊЬѕМўЪЧ![]() Чв
Чв![]()
Цфжае§ШЗУќЬтЕФађКХЪЧЃЈ ЃЉ
A. ЂйЂк B. ЂкЂл C. ЂлЂм D. ЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCЕФШ§ИіЖЅЕуAЃЈ4ЃЌЉ6ЃЉЃЌBЃЈЉ4ЃЌ0ЃЉЃЌCЃЈЉ1ЃЌ4ЃЉЃЌЧѓЃК
ЃЈ1ЃЉBCБпЕФДЙжБЦНЗжЯпEFЕФЗНГЬЃЛ
ЃЈ2ЃЉABБпЕФжаЯпЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌШєЧњЯп
ЃЌШєЧњЯп![]() ЃЈ
ЃЈ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЩЯДцдкЕу
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЩЯДцдкЕу![]() ЪЙЕУ
ЪЙЕУ![]() ЃЌдђЪЕЪ§
ЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЮЊ__________.
ЕФШЁжЕЗЖЮЇЮЊ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШєКЏЪ§![]() гы
гы![]() ЕФЭМЯѓЧЁКУЯрЧагыЕу
ЕФЭМЯѓЧЁКУЯрЧагыЕу![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=asinxЉbcosxЃЈaЁЂbЮЊГЃЪ§ЃЌaЁй0ЃЌxЁЪRЃЉдкx= ![]() ДІШЁЕУзюаЁжЕЃЌдђКЏЪ§y=fЃЈ
ДІШЁЕУзюаЁжЕЃЌдђКЏЪ§y=fЃЈ ![]() ЉxЃЉЪЧЃЈ ЃЉ
ЉxЃЉЪЧЃЈ ЃЉ
A.ХМКЏЪ§ЧвЫќЕФЭМЯѓЙигкЕуЃЈІаЃЌ0ЃЉЖдГЦ
B.ХМКЏЪ§ЧвЫќЕФЭМЯѓЙигкЕу ![]() ЖдГЦ
ЖдГЦ
C.ЦцКЏЪ§ЧвЫќЕФЭМЯѓЙигкЕу ![]() ЖдГЦ
ЖдГЦ
D.ЦцКЏЪ§ЧвЫќЕФЭМЯѓЙигкЕуЃЈІаЃЌ0ЃЉЖдГЦ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com