
【题目】已知函数![]() ,其中a∈R.
,其中a∈R.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,设
时,设![]() 、
、![]() 为曲线
为曲线![]() 上任意两点,曲线
上任意两点,曲线![]() 在点
在点![]() 处的切线斜率为k,证明:
处的切线斜率为k,证明:![]() .
.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题:
①“数列![]() 为等比数列”是“数列
为等比数列”是“数列![]() 为等比数列”的充分不必要条件;
为等比数列”的充分不必要条件;
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充要条件;
上为增函数”的充要条件;
③“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 互相垂直”的充要条件;
互相垂直”的充要条件;
④设![]() ,
,![]() ,
,![]() 分别是
分别是![]() 三个内角
三个内角![]() ,
,![]() ,
,![]() 所对的边,若
所对的边,若![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件.其中,真命题的序号是________.
”的必要不充分条件.其中,真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2sin x,
=(2sin x,![]() cos x),
cos x),![]() =(-sin x,2sin x),函数f(x)=
=(-sin x,2sin x),函数f(x)=![]() ·
·![]()
(1)求f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=1,c=1,ab=2![]() ,且a>b,求a,b的值.
,且a>b,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形ABDC中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
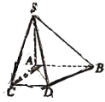
(1)若S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由;
(2)直角梯形ABDC绕直线AC所在直线旋转一周所得几何体名称是什么?并求出其体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() ,
,![]() ,给出下列曲线方程:(1)
,给出下列曲线方程:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,在曲线上存在点
,在曲线上存在点![]() 满足
满足![]() 的所有曲线是( )
的所有曲线是( )
A.(1)(2)(3)(4)B.(2)(3)
C.(1)(4)D.(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 与x轴,y轴的交点分别为A,B,圆C以线段AB为直径.
与x轴,y轴的交点分别为A,B,圆C以线段AB为直径.
(1)求圆C的标准方程;
(2)若直线l过点![]() 且圆心C到l的距离为1,求直线l的方程.
且圆心C到l的距离为1,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com