
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,记函数
,记函数![]() 的两个极值点为
的两个极值点为![]() ,
,![]() (其中
(其中![]() ),求
),求![]() 的最大值.
的最大值.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在
在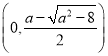 和
和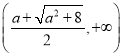 上单调递增,在
上单调递增,在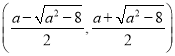 上单调递减;
上单调递减;
(2)![]() .
.
【解析】
(1)求出导函数![]() ,由
,由![]() 得增区间,由
得增区间,由![]() 得减区间,注意题中函数定义域是
得减区间,注意题中函数定义域是![]() ,因此对二次三项式
,因此对二次三项式![]() 分类情况为第一类:
分类情况为第一类:![]() 或
或![]() ,第二类
,第二类![]() 且
且![]() .
.
(2)与极值点有关的问题,不是直接代入极值点,而是用![]() 表示极值点,由
表示极值点,由![]() 是方程
是方程![]() 的解,得
的解,得![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]()
![]() .不妨设
.不妨设![]() ,引入变量
,引入变量![]() ,则
,则![]() ,
,![]() 就转化为
就转化为![]() 的函数,由
的函数,由![]() 求得
求得![]() 的范围,由导数知识可得所求最大值.
的范围,由导数知识可得所求最大值.
(1)![]() .
.
令![]() ,则
,则![]() .
.
①当![]() 或
或![]() ,即
,即![]() 时,得
时,得![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() ,即
,即![]() 时,
时,
由![]() ,得
,得![]() 或
或![]() ;
;
由![]() ,得
,得![]() .
.
∴函数![]() 在
在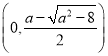 和
和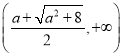 上单调递增,
上单调递增,
在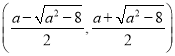 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在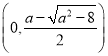 和
和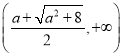 上单调递增,
上单调递增,
在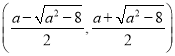 上单调递减.
上单调递减.
(2)由(1)得,当![]() 时,
时,![]() 有两极值点
有两极值点![]() ,
,![]() (其中
(其中![]() ).
).
则![]() ,
,![]() 为
为![]() 的两根,
的两根,
∴![]() ,
,![]() .
.
![]()
![]()
![]() .
.
令![]() ,
,
则![]() .
.
由![]() ,得
,得 ,
,
即![]() ,解得
,解得![]() .
.
∵![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
即![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在制造产品时需要用到长度为698mm的A型和长度为518mm的B型两种钢管,工厂利用长度为4000mm的钢管原材料,裁剪成若干A型和B型钢管。假设裁剪时损耗忽略不计,裁剪后所剩废料与原材料的百分比称为废料率.
(1)有两种裁剪方案的废料率小于4.5%,请说明这两种方案并计算它们的废料率;
(2)工厂现有100根原材料钢管,一根A型和一根B型钢管为一套毛胚。按(1)中的方案裁剪,最多可裁剪多少套毛胚?最终的废料率为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市10月1日至14日的空气质量指数趋势图,空气质量指数越小表示空气质量越好,空气质量指数小于100表示空气质量优良,下列叙述中不正确的是( )
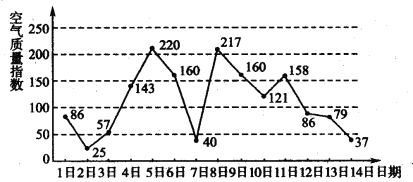
A.这14天中有7天空气质量优良
B.这14天中空气质量指数的中位数是103
C.从10月11日到10月14日,空气质量越来越好
D.连续三天中空气质量指数方差最大的是10月5日至10月7日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都是正数,其前
的各项都是正数,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,其中
,其中![]() ,常数
,常数![]()
![]() .
.
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个周期数列(存在正整数
是一个周期数列(存在正整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为周期数列,
为周期数列,![]() 为它的一个周期),求该数列的最小周期;
为它的一个周期),求该数列的最小周期;
(3)若数列![]() 是各项均为有理数的等差数列,
是各项均为有理数的等差数列,![]() (
(![]() ),问:数列
),问:数列![]() 中的所有项是否都是数列
中的所有项是否都是数列![]() 中的项?若是,请说明理由;若不是,请举出反例.
中的项?若是,请说明理由;若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,动点P与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离之比是
的距离之比是![]() ,设动点P的轨迹为E.
,设动点P的轨迹为E.
(1)求动点P的轨迹E的方程;
(2)设过F的直线交轨迹E的弦为AB,过原点的直线交轨迹E的弦为CD,若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com