练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】求定积分的值．

    【答案】【解答】表示圆(x-1)2+y2=1(y≥0)的一部分与直线y=x所围成的图形的面积，故原式=×π×12- ×1×1=
    【解析】利用定积分的几何意义求定积分的方法步骤：(1)确定被积函数和积分区间．(2)准确画出图形．(3)求出各部分的面积．(4)写出定积分，注意当f(x)≥0时，S= f(x)dx ， 而当f(x)≤0时，S=- f(x)dx ． ；利用定积分的几何意义求定积分的注意点：准确理解其几何意义，同时要合理利用函数的奇偶性．对称性来解决问题．另外，要注意结合图形的直观辅助作用．
    【考点精析】认真审题，首先需要了解定积分的概念(定积分的值是一个常数，可正、可负、可为零；用定义求定积分的四个基本步骤：①分割；②近似代替；③求和；④取极限)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标，现从700袋牛奶中抽取50袋进行检验．利用随机数表抽取样本时，先将700袋牛奶按001，002，…，700进行编号，如果从随机数表第3行第1组数开始向右读，最先读到的5袋牛奶的编号是614，593，379，242，203，请你以此方式继续向右读数，随后读出的3袋牛奶的编号是 ． （下列摘取了随机数表第1行至第5行）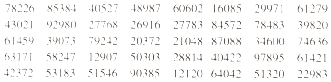

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，求曲线在点处的切线方程；

    （2）若函数在其定义域内为增函数，求的取值范围；

    （3）在（2）的条件下，设函数，若在上至少存在一点，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明命题“当n是正奇数时，xn＋yn能被x＋y整除”，在第二步的证明时，正确的证法是(　　)
    A.假设n＝k(k∈N*)时命题成立，证明n＝k＋1时命题也成立
    B.假设n＝k(k是正奇数)时命题成立，证明n＝k＋1时命题也成立
    C.假设n＝k(k是正奇数)时命题成立，证明n＝k＋2时命题也成立
    D.假设n＝2k＋1(k∈N)时命题成立，证明n＝k＋1时命题也成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知正四棱柱中，底面边长，侧棱 的长为4，过点作的垂线交侧棱于点，交于点．

    （1）求证： ⊥平面；

    （2）求二面角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 个正数 满足 （ 且 ）．
    （1）当 时，证明： ；
    （2）当 时，不等式 也成立，请你将其推广到 （ 且 ）个正数 的情形，归纳出一般性的结论并用数学归纳法证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为．

    （1）写出曲线的直角坐标方程；

    （2）已知点的直角坐标为，直线与曲线相交于不同的两点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=x2+2x．
    （Ⅰ）求f（0）的值；
    （Ⅱ）求此函数在R上的解析式；
    （Ⅲ）若对任意的t∈R，不等式f（t+1）+f（m﹣2t2）＜0恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|x2﹣3x+2=0}，B={x|x2﹣mx+m﹣1=0}若A∪B=A，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案