
【题目】关于![]() 的方程
的方程![]() 的解集中只含有一个元素,则
的解集中只含有一个元素,则![]() 的取值集合为______.
的取值集合为______.
科目:高中数学 来源: 题型:
【题目】某工厂家具车间做A,B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A,B型桌子分别需要1小时和2小时,漆工油漆一张A,B型桌子分别需要3小时和1小时;又知木工和漆工每天工作分别不得超过8小时和9小时,设该厂每天做A,B型桌子分别为x张和y张.
(1)试列出x,y满足的关系式,并画出相应的平面区域;
(2)若工厂做一张A,B型桌子分别获得利润为2千元和3千元,那么怎样安排A,B型桌子生产的张数,可使得所得利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第八章“方程”问题八:今有卖牛二、羊五,以买十三豕,有余钱一千。卖牛三、豕三,以买九羊,钱适足.卖羊六、豕八,以买五牛,钱不足六百.问牛、羊、豕各几何?“如果卖掉2头牛和5只羊,可买13口猪,还余1000钱;卖掉3头牛和3口猪的钱恰好可买9只羊;而卖掉6只羊和8口猪,去买5头牛,还少600钱.问牛、羊、猪的价格各是多少”.按照题意,可解出牛______钱、羊______钱、猪______钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把物体放在冷空气中冷却,如果物体原来的温度是![]() ,空气的温度是
,空气的温度是![]() ,则1min后物体的温度
,则1min后物体的温度![]() 可由公式
可由公式![]() 求得,其中k是常数,把温度是
求得,其中k是常数,把温度是![]() 的物体放在15℃的空气中冷却,1 min后,物体的温度是
的物体放在15℃的空气中冷却,1 min后,物体的温度是![]() .
.
(1)求出k的值;
(2)计算开始冷却多久后,上述物体的温度分别是![]() ;
;
(3)判断上述物体最终能否冷却到12℃,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:

如果A、B两个节目要相邻,且都不排在第3号位置,则节目单上不同的排序方式有( )种
A. 192 B. 144 C. 96 D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:
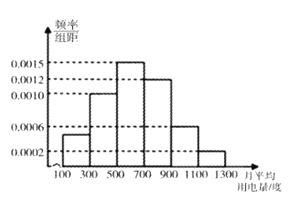
若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com