
【题目】已知函数![]()
![]() 在区间
在区间![]() 上单调递增,在区间
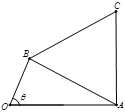
上单调递增,在区间![]() 上单调递减;如图,四边形
上单调递减;如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的内角
的内角![]() 的对边,
的对边,
且满足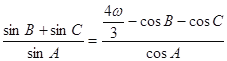 .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,设
,设![]() ,
,![]() ,
,
![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)正弦定理的运用根据边角的转换来得到证明。
(2)![]() 时取最大值,
时取最大值,![]() 的最大值为
的最大值为![]()
【解析】
试题分析:(1)利用两角和正弦公式和降幂公式化简,要熟练掌握公式,不要把符号搞错,很多同学化简不正确,求解较复杂三角函数的最值时,首先化成![]() 形式,在求最大值或最小值,寻求角与角之间的关系,化非特殊角为特殊角,灵活的掌握两角和的正弦公式进行化简;(2)在三角形中,处理三角形的边角关系时,一般全部化成角的关系,或全部化成边的关系,解决三角形问题时,注意角的范围;(3)把形如
形式,在求最大值或最小值,寻求角与角之间的关系,化非特殊角为特殊角,灵活的掌握两角和的正弦公式进行化简;(2)在三角形中,处理三角形的边角关系时,一般全部化成角的关系,或全部化成边的关系,解决三角形问题时,注意角的范围;(3)把形如![]() 化为
化为![]() ,可进一步研究函数的周期、单调性、最值和对称性.
,可进一步研究函数的周期、单调性、最值和对称性.
试题解析:解:(1)由题意知:![]() ,解得:
,解得:![]() ,
,
![]()
![]()
![]()
![]()
![]()
(2)因为![]() ,所以
,所以![]() ,所以
,所以![]() 为等边三角形
为等边三角形
![]()
![]()
![]()
![]() ,
,
![]() ,
,![]() ,
,
当且仅当![]() 即
即![]() 时取最大值,
时取最大值,![]() 的最大值为
的最大值为![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】某校参加夏令营的同学有3名男同学![]() 和3名女同学
和3名女同学![]() ,其所属年级情况如下表:
,其所属年级情况如下表:
高一年级 | 高二年级 | 高三三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母写出这个试验的样本空间;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件![]() 的样本点,并求事件
的样本点,并求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)的定义域为(0,+∞),且满足f(2)=1,f(xy)=f(x)+f(y),又当x2>x1>0时,f(x2)>f(x1).
(1)求f(1)、f(4)、f(8)的值;
(2)若有f(x)+f(x-2)≤3成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为![]() 的圆过原点
的圆过原点![]() ,且直线
,且直线![]() 与圆
与圆![]() 相切于点
相切于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.
两点.
①若![]() ,求弦
,求弦![]() 的长;
的长;
②若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求直线
成立,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极小值;
的极小值;
(2)设函数![]() ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量![]() 使得
使得![]() 的值相等,若存在,请求出
的值相等,若存在,请求出![]() 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com