练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    下面是2×2列联表:
     
    		y1
    		y2
    		总计
    x1
    		a
    		21
    		73
    x2
    		22
    		25
    		47
    总计
    		b
    		46
    		120
    则表中a,b的值分别为(　　)
    (A)94,72        (B)52,50
    (C)52,74        (D)74,52
    C
    ∵a+21=73,∴a=52,又a+22=b,
    ∴b=74.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    为了解高二某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：

    已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为.
    （1）请将上面的列联表补充完整；
    （2）是否有99.5%的把握认为喜爱打篮球与性别有关？说明你的理由；
    下面的临界值表供参考：

    (参考公式K2＝，其中n＝a＋b＋c＋d)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知与之间的几组数据如下表:

    		1
    		2
    		3
    		4
    		5
    		6

    		0
    		2
    		1
    		3
    		3
    		4
     
    假设根据上表数据所得线性回归直线方程为．若某同学根据上表中前两组数据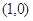和求得的直线方程为,则以下结论正确的是（ ）。
    A．   B．     C．    D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

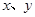    已知的取值如下表：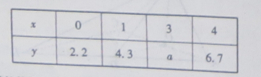

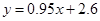    根据上表提供的数据，求出y对x的线性回归方程为，则表中的数据a的值为（   ）
    A．4.6B．4.8 C．5.45D．5.55

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    实验测得四组(x,y)的值分别为(1,2),(2,3),(3,4),(4,4)，则y与x间的线性回归方程是（ ）
    A．y＝－1＋xB．y＝1＋xC．y＝1.5＋0.7xD．y＝1＋2x

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
     
    		喜爱打篮球
    		不喜爱打篮球
    		总计
    男生
    		20
    		5
    		25
    女生
    		10
    		15
    		25
    总计
    		30
    		20
    		50
    则在犯错误的概率不超过　　　　的前提下认为喜爱打篮球与性别有关(请用百分数表示).
    附:χ2=
    P(χ2≥x0)
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001
    x0
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    对一些城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查后知,y与x具有相关关系,满足回归方程=0.66x+1.562.若某被调查城市的居民人均消费水平为7.675(千元),则可以估计该城市人均消费额占人均工资收入的百分比约为　　　　%(结果保留两个有效数字).

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验.根据收集到的数据（如下表），由最小二乘法求得回归直线方程，表中有一个数据模糊不清，请你推断出该数据的值为(    )
    A．75B．62C．68D．81

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    回归直线方程=，其中样本中心点为（1,2 ）则回归直线方程为（  ）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案