
分析 (1)不等式f(x)>8可化为:3x2-6x-9>0,即x2-2x-3>0,解得答案;
(2)若任意x∈R,都有g(x)<0,则△=(m-6)2-16<0,解得m的取值范围;
(3)若对于任意的a∈[1,2],关于x的不等式f(x)≤x2-(2a+6)x+a+b+4在区间[1,3]的解集非空,则不等式2x2+2ax-(a+b+5)≤0在区间[1,3]的解集非空,构造函数ϕ(x)=2x2+2ax-(a+b+5),求其最小值,可得实数b的取值范围.
解答 解:(1)不等式f(x)>8可化为:3x2-6x-9>0,
即x2-2x-3>0,
解得:x<-1或x>3,
故原不等式的解集为:{x|x<-1或x>3};
(2)g(x)=f(x)-4x2+mx-3=-x2+(m-6)x-4,
若任意x∈R,都有g(x)<0,
则△=(m-6)2-16<0,
解得:2<m<10;
(3)若对于任意的a∈[1,2],关于x的不等式f(x)≤x2-(2a+6)x+a+b+4在区间[1,3]的解集非空,
则对于任意的a∈[1,2],关于x的不等式2x2+2ax-(a+b+5)≤0在区间[1,3]的解集非空,
令ϕ(x)=2x2+2ax-(a+b+5),则函数图象的对称轴为直线$x=-\frac{a}{2}$,
由$-\frac{a}{2}∈[-1,-\frac{1}{2}]$得:ϕmin(x)=ϕ(1)=a-b-3,
所以只要当a∈[1,2]时,a-b-3≤0恒成立即可
即当a∈[1,2]时,b≥a-3恒成立,
所以实数b的取值范围是[-1,+∞).
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
已知 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 的前
的前 项和,则
项和,则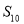 的值为( )
的值为( )
A.-110 B.-90 C.90 D.110
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 16 | C. | 9 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
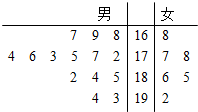 从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.
从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{2}{3}$n+$\frac{1}{3}$ | B. | an=$\frac{2}{3}$n-$\frac{1}{3}$ | C. | an=$\frac{1}{3}$n+$\frac{1}{3}$ | D. | an=$\frac{2}{3}$n+$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com