
【题目】现有4个人参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求出4个人中恰有2个人去 参加甲游戏的概率;
(2)求这4个人中去参加甲游戏人数大于去参加乙游戏的人数的概率;
(3)用 ![]() 分别表示这4个人中去参加甲、乙游戏的人数,记
分别表示这4个人中去参加甲、乙游戏的人数,记 ![]() ,求随机变量
,求随机变量 ![]() 的分布列与数学期望
的分布列与数学期望 ![]() .
.
科目:高中数学 来源: 题型:
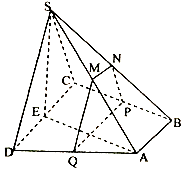
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若 ![]() =t
=t ![]() .
. 
(1)当t= ![]() 时,求证:平面SAE⊥平面MNPQ;
时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M﹣PQ﹣A的平面角的余弦值为 ![]() ?若存在,求出实数t的值;若不存在,说明理由.
?若存在,求出实数t的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 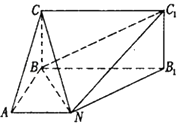
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知不等式ax2-3x+6>4的解集为{x|x<1或x>b},
(1)求a,b;
(2)解不等式ax2-(ac+b)x+bc<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. 
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ![]() ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为- ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ;
;
(1)若函数 ![]() 在
在 ![]() 上为增函数,求正实数
上为增函数,求正实数 ![]() 的取值范围;
的取值范围;
(2)当 ![]() 时,求函数
时,求函数 ![]() 在
在 ![]() 上的最值;
上的最值;
(3)当 ![]() 时,对大于1的任意正整数
时,对大于1的任意正整数 ![]() ,试比较
,试比较 ![]() 与
与 ![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,![]() =2
=2![]() =2.
=2.
(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
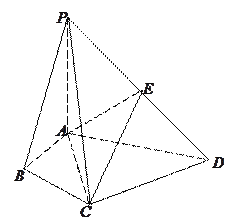
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com