
【题目】某同学理科成绩优异,今年参加了数学,物理,化学,生物4门学科竞赛.已知该同学数学获一等奖的概率为![]() ,物理,化学,生物获一等奖的概率都是
,物理,化学,生物获一等奖的概率都是![]() ,且四门学科是否获一等奖相互独立.
,且四门学科是否获一等奖相互独立.
(1)求该同学至多有一门学科获得一等奖的概率;
(2)用随机变量![]() 表示该同学获得一等奖的总数,求
表示该同学获得一等奖的总数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平行四边形OABC,顶点O,A,C分别表示0,3+2i,-2+4i,试求:
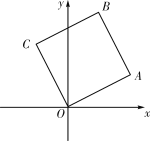
(1) ![]() 所表示的复数;
所表示的复数;
(2)对角线![]() 所表示的复数;
所表示的复数;
(3)B点对应的复数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第八章“方程”问题八:今有卖牛二、羊五,以买十三豕,有余钱一千。卖牛三、豕三,以买九羊,钱适足.卖羊六、豕八,以买五牛,钱不足六百.问牛、羊、豕各几何?“如果卖掉2头牛和5只羊,可买13口猪,还余1000钱;卖掉3头牛和3口猪的钱恰好可买9只羊;而卖掉6只羊和8口猪,去买5头牛,还少600钱.问牛、羊、猪的价格各是多少”.按照题意,可解出牛______钱、羊______钱、猪______钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,食甚时刻为21时31分,22时08分生光,直至23时12分复圆.全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”将在食甚时刻开始,生光时刻结東,一市民准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求弦长
两点,求弦长![]() ,若点
,若点![]() ,求
,求![]() 的值;
的值;
(2)以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 和圆
和圆![]() 的交点为
的交点为![]() ,
,![]() ,求弦
,求弦![]() 所在直线的直角坐标方程.
所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com