练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设双曲线C：的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q。

       （Ⅰ）若直线m与x轴正半轴的交点为T，且，求点T的坐标；

       （Ⅱ）求直线A1P与直线A2Q的交点M的轨迹E的方程；

       （Ⅲ）过点F（1，0）作直线l与（Ⅱ）中的轨迹E交于不同的两点A、B，设，若（T为（Ⅰ）中的点）的取值范围。

    （Ⅰ）点T的坐标为（2，0）

    （Ⅱ）

    （Ⅲ）


    解析:

    （Ⅰ）由题，得，设

    则

    由  …………①

    又在双曲线上，则   …………②

    联立①、②，解得    

    由题意，

    ∴点T的坐标为（2，0）   …………3分

    （Ⅱ）设直线A1P与直线A2Q的交点M的坐标为（x，y）

    由A1、P、M三点共线，得

       …………③  …………1分

    由A2、Q、M三点共线，得

       …………④  …………1分

    联立③、④，解得    …………1分

    ∵在双曲线上，

    ∴

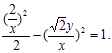
    ∴轨迹E的方程为  …………1分

    （Ⅲ）容易验证直线l的斜率不为0。

    故可设直线l的方程为  中，得

      

    设

    则由根与系数的关系，得  ……⑤

      ……⑥   …………2分

    ∵ ∴有

    将⑤式平方除以⑥式，得

       …………1分

    由

      …………1分

    ∵

    又

    故

    令    ∴，即

    ∴

    而 ，  ∴

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014届重庆市高二上学期期中考试理科数学试卷（解析版） 题型：解答题

    设双曲线C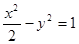：的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点。

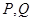    （1）若直线m与x轴正半轴的交点为T，且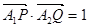，求点T的坐标；

    （2）求直线A1P与直线A2Q的交点M的轨迹E的方程；

    （3）过点F（1，0）作直线l与（Ⅱ）中的轨迹E交于不同的两点A、B，设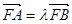，若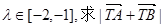（T为（1）中的点）的取值范围。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设双曲线C:=1的左、右焦点分别为F1、F2，点P是双曲线位于第一象限内的一个点，且满足·=0,则△PF1F2的内切圆的方程为

    A.(x-2)2+(y-1)2=1                             B.(x-3)2+(y-2)2=4

    C.(x-3)2+(y-1)2=1                             D.(x-4)2+(y-2)2=4

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省西安中学高考数学第十三次模拟试卷（理科）（解析版） 题型：选择题

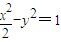    设双曲线C：的左、右顶点分别为A1、A2，垂直于x轴的直线l与双曲线C交于不同的两点P、Q．若直线l与x轴正半轴的交点为M，且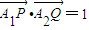，则点M的坐标为（ ）
    A．（，0）
    B．（2，0）
    C．（，0）
    D．（3，0）

    查看答案和解析>>

    科目：高中数学 来源：江西省上高二中09-10学年高二第五次月考（理） 题型：解答题

     设双曲线C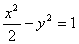：的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q。

    （Ⅰ）若直线m与x轴正半轴的交点为T，且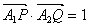，求点T的坐标；

    （Ⅱ）求直线A1P与直线A2Q的交点M的轨迹E的方程；

     

     

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案