
【题目】如图1,四边形ABCD中,AB∥CD,AD⊥AB,AB=2CD=4,AD=2,过点C作CO⊥AB,垂足为O,将△OBC沿CO折起,如图2使得平面CBO与平面AOCD所成的二面角的大小为θ(0<θ<π),E,F分别为BC,AO的中点 
(1)求证:EF∥平面ABD
(2)若θ= ![]() ,求二面角F﹣BD﹣O的余弦值.
,求二面角F﹣BD﹣O的余弦值.
【答案】
(1)证明:过点E作EH∥BD,交CD于点H,连结HF,
则H为CD中点,∴HF∥AD
∵AD平面ABD,HF平面ABD,
∴HF∥平面ABD,
同理,EH∥平面ABD,
∵EH∩HF=H,∴平面EHF∥平面ABD,
∵EF平面EHF,∴EF∥平面ABD
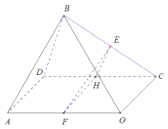
(2)解:由题得平面CBO与平面AOCD所成二面角的平面角为∠BOA=θ,
连结BF,∵θ= ![]() ,OB=2,OF=1,∴BF⊥AO,
,OB=2,OF=1,∴BF⊥AO,
以点F为坐标原点,以FO,FH,FB分别为x,y,z轴,建立空间直角坐标系,
则F(0,0,0),B(0,0, ![]() ),D(﹣1,2,0),O(1,0,0),
),D(﹣1,2,0),O(1,0,0),
设平面FBD的法向量 ![]() =(x,y,z),
=(x,y,z),
则 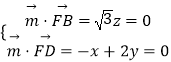 ,取x=2,解得
,取x=2,解得 ![]() =(2,﹣1,0)
=(2,﹣1,0)
同理得平面BDO的一个法向量 ![]() =(
=( ![]() ,1),
,1),
设二面角F﹣BD﹣O的平面角为α,
cosα= ![]() =
= ![]() =
= ![]() ,
,
∴二面角F﹣BD﹣O的余弦值为 ![]() .
.
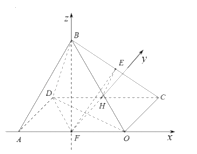
【解析】(1)过点E作EH∥BD,交CD于点H,连结HF,推导出平面EHF∥平面ABD,由此能证明EF∥平面ABD.(2)由题得平面CBO与平面AOCD所成二面角的平面角为∠BOA=θ,连结BF,以点F为坐标原点,以FO,FH,FB分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣BD﹣O的余弦值.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行. 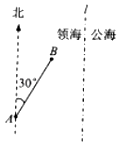
(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°≈ ![]() ,
, ![]() ≈5.7446)
≈5.7446)
(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣1|﹣|x+2|.
(Ⅰ)解不等式f(x)>0;
(Ⅱ)若x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为  (t为参数)以坐标原点O为极点,x轴的正半轴为极轴的极坐标系.
(t为参数)以坐标原点O为极点,x轴的正半轴为极轴的极坐标系.
(1)写出直线l的普通方程以及曲线C的极坐标方程;
(2)若直线l与曲线C的两个交点分别为M,N,直线l与x轴的交点为P,求|PM||PN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的可导函数f(x)的导函数为f′(x),若f(3)=1,且3f(x)+xf′(x)>ln(x+1),则不等式(x﹣2017)3f(x﹣2017)﹣27>0的解集为( )
A.(2014,+∞)
B.(0,2014)
C.(0,2020)
D.(2020,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.
(1)求证:DE∥平面PAC;
(2)求证:DE⊥AD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某算法的程序框图,若程序运行后输出的结果是14,则判断框内填入的条件可以是( ) 
A.S≥10?
B.S≥14?
C.n>4?
D.n>5?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年美国总统大选过后,有媒体从某公司的全体员工中随机抽取了200人,对他们的投票结果进行了统计(不考虑弃权等其他情况),发现支持希拉里的一共有95人,其中女员工55人,支持特朗普的男员工有60人.
(Ⅰ)根据已知条件完成下面的2×2列联表:据此材料,是否有95%的把握认为投票结果与性别有关?
支持希拉里 | 支持特朗普 | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(Ⅱ)若从该公司的所有男员工中随机抽取3人,记其中支持特朗普的人数为X,求随机变量X的分布列和数学期望.(用相应的频率估计概率)
附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣7|+1.
(1)求不等式f(x)≤x的解集;
(2)若存在x使不等式f(x)﹣2|x﹣1|≤a成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com