
选做题.(本题满分10分.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.)
选修4—1:平面几何
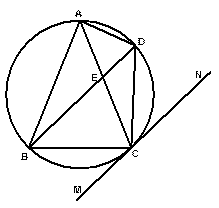
如图,Δ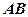
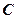 是内接于⊙O,
是内接于⊙O,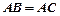 ,直线
,直线 切⊙O于点
切⊙O于点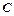 ,弦
,弦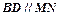 ,
,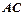 与
与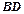 相交于点
相交于点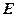 .
.
(1)求证:Δ ≌Δ
≌Δ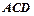 ;
;
(2)若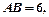
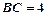 ,求
,求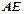 .
.
解:(Ⅰ)在ΔABE和ΔACD中,
∵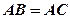 ∠ABE=∠ACD………………2分
∠ABE=∠ACD………………2分
又,∠BAE=∠EDC
∵BD//MN
∴∠EDC=∠DCN
∵直线是圆的切线,
∴∠DCN=∠CAD
∴∠BAE=∠CAD
∴Δ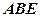
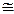 Δ
Δ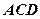 (角、边、角)……………………………5分
(角、边、角)……………………………5分
(Ⅱ)∵∠EBC=∠BCM ∠BCM=∠BDC[来源:学+科+网Z+X+X+K]
∴∠EBC=∠BDC=∠BAC BC=CD=4
又 ∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB
∴ BC="BE=4 " ……………………………8分
设AE=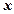 ,易证 ΔABE∽ΔDEC[来源:学+科+网]
,易证 ΔABE∽ΔDEC[来源:学+科+网]
∴
又 
∴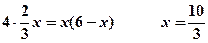 ……………………………10分
……………………………10分
解析


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
选修4—1:几何证明选讲(10分):
如图:如图E、F、G、H为凸四边形ABCD中AC、BD、AD、DC的中点,∠ABC=∠ADC。
(1)求证:∠ADC=∠GEH; (3分)
(2)求证:E、F、G、H四点共圆; (4分)
(3)求证:∠AEF=∠ACB-∠ACD (3分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,现在要在一块半径为1m.圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设∠BOP=θ,YMNPQ的面积为S.
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应θ的值
1. 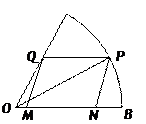
2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分) 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。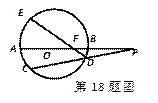
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,AD=2AB=2,∠BAD=60º,M、N分别是对角线BD、AC上的点,AC、BD相交于点O,已知BM= BO,ON=
BO,ON= OC.设向量
OC.设向量 =a,
=a, =b
=b


(1)试用a,b表示 ;w
;w
(2)求| |.
|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com