分析:(Ⅰ)由三棱柱ABC-A
1B
1C
1为正三棱柱,取BC边的中点O,连结AO,可证AO垂直于底面,以O为坐标原点建立空间直角坐标系,由已知求出各点的坐标,得到向量
,,的坐标,由向量的数量积等于0可证AB
1⊥平面A
1BD;
(Ⅱ)把D点的坐标用含有λ的代数式表示,求出二面角A-A
1D-B的两个面的法向量,利用法向量所成的角为
即可得到λ的值.
解答: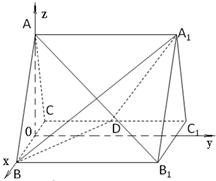
(Ⅰ)证明:取BC的中点为O,连结AO
在正三棱柱ABC-A
1B
1C
1中,面ABC⊥面CB
1,△ABC为正三角形,所以AO⊥BC,
故AO⊥平面CB
1.
以O为坐标原点建立如图空间直角坐标系O-xyz.
则
A(0,0,),B
1(1,2,0),D(-1,1,0),
A1(0,2,),B(1,0,0).
所以
=(1,2,-),
=(1,1,),
=(2,-1,0),
因为
•=1+2-3=0,•=2-2=0,
所以AB
1⊥DA
1,AB
1⊥DB,又DA
1∩DB=D,
所以AB
1⊥平面A
1BD;
(Ⅱ)解:由(1)得D(-1,2λ,0),所以
=(1,2-2λ,),
=(2,-2λ,0),
=(1,-2λ,),
设平面A
1BD的法向量
=(x,y,z),平面AA
1D的法向量
=(s,t,u),
由
,得
,取y=1,得x=λ,
z=.
所以平面A
1BD的一个法向量为
=(λ,1,),
由
,得
,取u=-1,得x=
,y=0.
所以平面AA
1D的一个法向量
=(,0,-1),
由
cos<,>==,得
=
.
解得
λ=,为所求.
点评:本题考查了直线与平面垂直的判定,考查了二面角的平面角.训练了利用平面法向量求二面角的大小,是中档题.

 (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2, (Ⅰ)证明:取BC的中点为O,连结AO
(Ⅰ)证明:取BC的中点为O,连结AO

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f'(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )
(2013•郑州二模)函数f(x)的定义域为开区间(a,b),导函数f'(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( )