
【题目】已知长方体![]() ,
,![]() ,
,![]() ,
,![]() ,已知P是矩形
,已知P是矩形![]() 内一动点,
内一动点,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,设P点形成的轨迹长度为
,设P点形成的轨迹长度为![]() ,则
,则![]() _________;当
_________;当![]() 的长度最短时,三棱锥
的长度最短时,三棱锥![]() 的外接球的表面积为_____________.
的外接球的表面积为_____________.
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高,2019年全年总收入与2018年全年总收入相比增长了一倍,同时该企业的各项运营成本也随着收入的变化发生相应变化,下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法错误的是( )
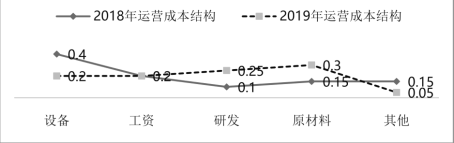
A.该企业2019年研发的费用与原材料的费用超过当年总收入的50%
B.该企业2019年设备支出金额及原材料的费用均与2018相当
C.该企业2019年工资支出总额比2018年多一倍
D.该企业2018年与2019研发的总费用占这两年总收入的20%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为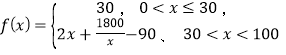 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代重要建筑的室内上方,通常会在正中部位做出向上凸起的窟窿状装饰,这种装饰称为藻井.北京故宫博物院内的太和殿上方即有藻井(图1),全称为龙风角蝉云龙随瓣枋套方八角深金龙藻井.它展示出精美的装饰空间和造型艺术,是我国古代丰富文化的体现,从分层构造上来看,太和殿藻井由三层组成:最下层为方井,中为八角井,上为圆井.图2是由图1抽象出的平面图形,若在图2中随机取一点,则此点取自圆内的概率为( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/18/2487522753945600/2488179565256704/STEM/4d65bbaaf0c447efbbb2157ff8983df0.png]
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为直径的圆
为直径的圆![]() .当
.当![]() 时,圆
时,圆![]() 的半径为2.
的半径为2.
(1)求![]() 的方程;
的方程;
(2)已知点![]() ,对任意的斜率
,对任意的斜率![]() ,圆
,圆![]() 上是否总存在点
上是否总存在点![]() 满足
满足![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为1的正方形区域OABC内有以OA为半径的圆弧![]() .现决定从AB边上一点D引一条线段DE与圆弧
.现决定从AB边上一点D引一条线段DE与圆弧![]() 相切于点E,从而将正方形区域OABC分成三块:扇形COE为区域I,四边形OADE为区域II,剩下的CBDE为区域III.区域I内栽树,区域II内种花,区域III内植草.每单位平方的树、花、草所需费用分别为
相切于点E,从而将正方形区域OABC分成三块:扇形COE为区域I,四边形OADE为区域II,剩下的CBDE为区域III.区域I内栽树,区域II内种花,区域III内植草.每单位平方的树、花、草所需费用分别为![]() 、
、![]() 、
、![]() ,总造价是W,设
,总造价是W,设![]()

(1)分别用![]() 表示区域I、II、III的面积;
表示区域I、II、III的面积;
(2)将总造价W表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(3)求![]() 为何值时,总造价W取最小值?
为何值时,总造价W取最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,以下结论:
上的动点,以下结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③三棱锥![]() ,体积不变;
,体积不变;
④![]() 为
为![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大.
所成角最大.
其中正确的序号为( )
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com