
【题目】已知函数![]() 关于
关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,若
,若![]() ,则
,则![]() 的取值范围是________.
的取值范围是________.
【答案】![]()
【解析】
作出y=f(x)的图象,由题意可得f(x)<m(x+2)+2,作出直线y=m(x+2)+2,其恒过定点(﹣2,2),结合题意可得m<0,考虑直线经过点(0,1)和与直线y=1﹣4x平行的情况,再通过旋转即可得到m的范围.当x≤﹣1时和当x>﹣1时,分别解方程,x2+6x+10﹣mx﹣2m﹣2=0,即x2+(6﹣m)x+8﹣2m=0的两个实根x1,x2;x1+x2=m﹣6;方程﹣4x+1﹣mx﹣2m﹣2=0的实根是x3;用m表示x1+x2+x3,根据m的取值范围解出即可.
画出函数y=f(x)的图象,
关于x的不等式f(x)﹣mx﹣2m﹣2<0,
即为f(x)<m(x+2)+2,
作出直线y=m(x+2)+2,其恒过定点(﹣2,2),
由解集是(x1,x2)∪(x3,+∞),
若x1x2x3>0,
可得x1<0,x2<0,x3>0,
当x≤﹣1时,x1,x2,是方程x2+6x+10﹣mx﹣2m﹣2=0的两个实根;
即x2+(6﹣m)x+8﹣2m=0的两个实根,∴x1+x2=m﹣6;
当x>﹣1时,x3是方程﹣4x+1﹣mx﹣2m﹣2=0的实根;
∴x3![]() ;
;
∴结合图象可得m<0,
当直线y=m(x+2)+2经过(0,1)时,可得2m+2=1,
解得m![]() ;
;
当直线y=m(x+2)+2与直线y=1﹣4x平行时,
m=﹣4.
由![]() 可得﹣4<m
可得﹣4<m![]() .
.
∴m+4>0,
则![]()
![]()
![]()
![]() 2
2![]() 12=2
12=2![]() 12;
12;
当且仅当m+4![]() 时,即m=﹣4
时,即m=﹣4![]() 时取等号;
时取等号;
故答案为:[2![]() 12,+∞).
12,+∞).



科目:高中数学 来源: 题型:
【题目】如图所示为一名曰“堑堵”的几何体,已知 AE⊥底面BCFE , DF ∥ AE , DF = AE = 1, CE =![]() ,四边形ABCD 是正方形.
,四边形ABCD 是正方形.

(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑.判断四面体 EABC 是否为鳖臑,若是,写出其 每一个面的直角,并证明;若不是,请说明理由.
(2)求四面体 EABC 的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
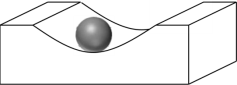
【题目】一个工业凹槽的轴截面是双曲线的一部分,它的方程是![]() ,在凹槽内放入一个清洁钢球(规则的球体),要求清洁钢球能擦净凹槽的最底部,则清洁钢球的最大半径为________.
,在凹槽内放入一个清洁钢球(规则的球体),要求清洁钢球能擦净凹槽的最底部,则清洁钢球的最大半径为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备投产一种新产品,经测算,已知每年生产![]() 万件的该种产品所需要的总成本
万件的该种产品所需要的总成本![]() (万元),依据产品尺寸,产品的品质可能出现优、中、差三种情况,随机抽取了1000件产品测量尺寸,尺寸分别在
(万元),依据产品尺寸,产品的品质可能出现优、中、差三种情况,随机抽取了1000件产品测量尺寸,尺寸分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:
(单位:![]() )中,经统计得到的频率分布直方图如图所示.
)中,经统计得到的频率分布直方图如图所示.
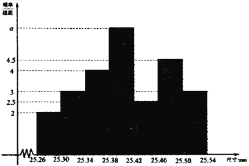
产品的品质情况和相应的价格![]() (元/件)与年产量
(元/件)与年产量![]() 之间的函数关系如下表所示.
之间的函数关系如下表所示.
产品品质 | 立品尺寸的范围 | 价格 |
优 |
|
|
中 |
|
|
差 |
|
|
以频率作为概率解决如下问题:
(1)求实数![]() 的值;
的值;
(2)当产量![]() 确定时,设不同品质的产品价格为随机变量
确定时,设不同品质的产品价格为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列;
的分布列;
(3)估计当年产量![]() 为何值时,该公司年利润最大,并求出最大值.
为何值时,该公司年利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,点
,点![]()
(1)求点![]() 与抛物线
与抛物线![]() 的焦点
的焦点![]() 的距离;
的距离;
(2)设斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)是否存在定圆![]() ,使得过曲线
,使得过曲线![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的两条切线,与曲线
的两条切线,与曲线![]() 交于另外两点
交于另外两点![]() 时,总有直线
时,总有直线![]() 也与圆
也与圆![]() 相切?若存在,求出
相切?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纪念章从某年某月某日起开始上市,通过市场调査,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数计,从下列函数中选取一个恰当的函数描述该纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系并说明理由:①
的变化关系并说明理由:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.![]() ,且
,且![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 与函数
与函数![]() 在公共点
在公共点![]() 处有相同的切线,且
处有相同的切线,且![]() 在
在![]() 上恒成立.
上恒成立.
(i)求![]() 和
和![]() 的值;(
的值;(![]() 为函数
为函数![]() 的导函数)
的导函数)
(ii)求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于具有相同定义域D的函数![]() 和
和![]() ,若存在函数
,若存在函数![]() (k,b为常数),对任给的正数m,存在相应的
(k,b为常数),对任给的正数m,存在相应的![]() ,使得当
,使得当![]() 且
且![]() 时,总有
时,总有![]() ,则称直线
,则称直线![]() 为曲线
为曲线![]() 和
和![]() 的“分渐近线”.给出定义域均为
的“分渐近线”.给出定义域均为![]() 的四组函数如下:
的四组函数如下:
①![]() ,
,![]() ;
;
②![]() ,
,![]() ;
;
③![]() ,
,![]() ;
;
④![]() ,
,![]()
其中,曲线![]() 和
和![]() 存在“分渐近线”的是________.
存在“分渐近线”的是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com