
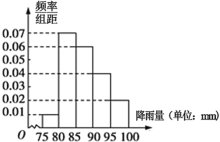
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:
若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
【答案】(1)87.25![]() ; (2)
; (2)![]() 小时,见解析.
小时,见解析.
【解析】
(1)先分别算出五组数据数据对应的频率,再利用平均数公式求解.
(2)先根据频率分布直方图得到一级警戒和二级警戒的时间数,用![]() 表示一级警戒的小时数,列出
表示一级警戒的小时数,列出![]() 的可能取值,再分别求得其概率,列出分布列,然后代入期望公式求解.
的可能取值,再分别求得其概率,列出分布列,然后代入期望公式求解.
(1)这五组数据对应的频率分别为:0.05,0.35,0.3,0.2,0.1.
故这100小时的平均降雨量为:
0.05×77.5+0.35×82.5+0.3×87.5+0.2×92.5+0.1×97.5=87.25![]() .
.
(2)由频率分步直方图可知,属于一级警戒的频率为:(0.04+0.02)×5=0.3,
则属于二级警戒的频率为1-0.3=0.7.所以,抽取的这10个小时中,
属于一级警戒的有3小时,属于二级警戒的有7小时.
从这10小时中抽取3小时,用![]() 表示一级警戒的小时数,
表示一级警戒的小时数,![]() 的取值可能为0,1,2,3.
的取值可能为0,1,2,3.
则![]() ,,
,,![]() .
.
所以,![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
则![]() 的期望值为:
的期望值为:![]() (小时).
(小时).


科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
:![]() (
(![]() )上,且点
)上,且点![]() 到左焦点
到左焦点![]() 的距离为3.
的距离为3.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 关于坐标原点
关于坐标原点![]() 的对称点为
的对称点为![]() ,又
,又![]()
![]() 两点在椭圆
两点在椭圆![]() 上,且
上,且![]() ,求凸四边形
,求凸四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,
的左、右焦点, ![]() 为双曲线的左顶点,以
为双曲线的左顶点,以![]() ,
, ![]() 为直径的圆交双曲线某条渐近线于
为直径的圆交双曲线某条渐近线于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,则该双曲线的离心率为________.
,则该双曲线的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前n项和为
的前n项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…有如下运算和结论:①
,…有如下运算和结论:①![]() ;②数列
;②数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列;③数列
,…是等比数列;③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .其中正确的结论是_____.(将你认为正确的结论序号都填上)
.其中正确的结论是_____.(将你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济全球化信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引留住培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
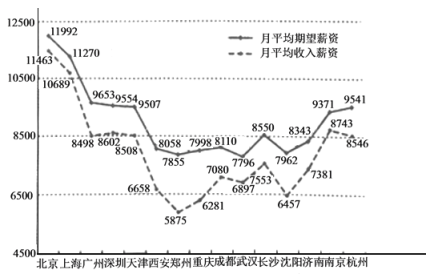
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)若从月平均收入薪资与月平均期望薪资之差高于1000元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都低于8500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在讨论勾股定理的过程中,《九章算术》提供了许多整勾股数,如![]() ,等等.其中最大的数称为“弦数”,后人在此基础上进一步研究,得到如下规律:若勾股数组中的某一个数
,等等.其中最大的数称为“弦数”,后人在此基础上进一步研究,得到如下规律:若勾股数组中的某一个数![]() 是确定的奇数(大于1),把它平方后拆成相邻的两个整数,那么奇数与这两个整数构成一组勾股数,若勾股数组中的某一个数
是确定的奇数(大于1),把它平方后拆成相邻的两个整数,那么奇数与这两个整数构成一组勾股数,若勾股数组中的某一个数![]() 是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数.由此得到的这种勾股数称之为“由
是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数.由此得到的这种勾股数称之为“由![]() 生成的一组勾股数”.若“由17生成的这组勾股数”的“弦数”为
生成的一组勾股数”.若“由17生成的这组勾股数”的“弦数”为![]() ,“由20生成的这组勾股数”的“弦数”为
,“由20生成的这组勾股数”的“弦数”为![]() ,则
,则![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() ).
).
(1)点![]() 的直角坐标为(2,2),且点
的直角坐标为(2,2),且点![]() 在曲线
在曲线![]() 内,求实数m的取值范围;
内,求实数m的取值范围;
(2)若![]() ,当
,当![]() 变化时,求直线被曲线
变化时,求直线被曲线![]() 截得的弦长的取值范围.
截得的弦长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近日,据《三秦都市报》消息称陕西新高考方案初稿已经形成,新高考从2019年秋季入学的新高一学生开始执行“3+3”模式,即除语文、数学、外语三科为必考科目外,还要在物理、化学、生物、历史、地理、政治六科中选择三科作为选考科目.已知某生的高考志愿定为北京大学环境科学专业,按照2018年北大高考招生选考科目要求物理、化学必选,为该生安排课表(上午四节、下午四节,每门课每天至少一节课),现该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻(上午第四节和下午第一节不算相邻),则该生该天课表不同的排法有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() .
.
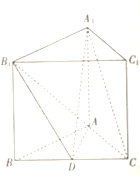
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,试问:
,试问:![]() 是否与平面
是否与平面![]() 平行?若平行,求三棱锥
平行?若平行,求三棱锥![]() 的体积;若不平行,请说明理由.
的体积;若不平行,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com