
【题目】已知数列{an}的前n项和为Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通项公式;
(2)数列{cn}满足cn=anbn , 求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
【答案】
(1)解:由Tn= ![]() n2﹣
n2﹣ ![]() n,易得an=3n﹣2代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简bn=
n,易得an=3n﹣2代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简bn= ![]() (n∈N*),
(n∈N*),
(2)解:cn=anbn= ![]() ,∴
,∴ ![]() ∴
∴ ![]()
两式相减整理得 ![]()
(3)解:cn=anbn=(3n﹣2) ![]() ∴cn+1﹣cn=(3n+1)
∴cn+1﹣cn=(3n+1) ![]() ﹣(3n﹣2)
﹣(3n﹣2) ![]() =9(1﹣n)
=9(1﹣n) ![]() (n∈N*),
(n∈N*),
∴当n=1时,c2=c1= ![]() ,
,
当n≥2时,cn+1<cn,即c1=c2>c3>…>cn,
∴当n=1时,cn取最大值是 ![]() ,又cn≤
,又cn≤ ![]() m2+m﹣1对一切正整数n恒成立∴
m2+m﹣1对一切正整数n恒成立∴ ![]() m2+m﹣1≥
m2+m﹣1≥ ![]() ,即m2+4m﹣5≥0,
,即m2+4m﹣5≥0,
解得:m≥1或m≤﹣5.
【解析】(1)由Tn= ![]() n2﹣
n2﹣ ![]() n,先求数列{an}的通项公式;代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简即可求出{bn}的通项公式;(2)把第一问求出的两数列的通项公式代入cn=anbn中,确定出cn的通项公式,从而求数列{cn}的前n项和Sn;(3)表示出cn+1﹣cn , 判断得到其差小于0,故数列{cn}为递减数列,令n=1求出数列{cn}的最大值,然后原不等式的右边大于等于求出的最大值,列出关于m的一元二次不等式,求出不等式的解集即为实数m的取值范围.
n,先求数列{an}的通项公式;代入到an+2+3log4bn=0(n∈N*)根据对数的运算性质化简即可求出{bn}的通项公式;(2)把第一问求出的两数列的通项公式代入cn=anbn中,确定出cn的通项公式,从而求数列{cn}的前n项和Sn;(3)表示出cn+1﹣cn , 判断得到其差小于0,故数列{cn}为递减数列,令n=1求出数列{cn}的最大值,然后原不等式的右边大于等于求出的最大值,列出关于m的一元二次不等式,求出不等式的解集即为实数m的取值范围.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系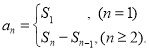 .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:
【题目】一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 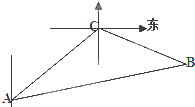
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
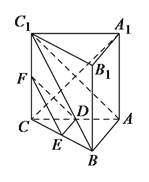
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若线段![]() 上的点
上的点![]() 满足平面
满足平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并说明理由.
的位置,并说明理由.
(Ⅲ)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|cosx|sinx,给出下列四个说法:
①f(x)为奇函数; ②f(x)的一条对称轴为x= ![]() ;
;
③f(x)的最小正周期为π; ④f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
⑤f(x)的图象关于点(﹣ ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为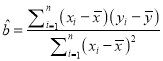 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com