
【题目】若洗水壶要用 1 分钟、烧开水要用 10 分钟、洗茶杯要用 2 分钟、取茶叶要用 1 分钟、 沏茶 1 分钟,那么较合理的安排至少也需要 ( )
A. 10分钟 B. 11分钟 C. 12分钟 D. 13分钟
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据绘制茎叶图,从茎叶图看,哪种药的疗效更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于在区间![]() 上有意义的两个函数
上有意义的两个函数![]() 与
与![]() ,如果对任意的
,如果对任意的![]() ,均有
,均有![]() ,则称
,则称![]() 与
与![]() 在
在![]() 上是接近的,否则称
上是接近的,否则称![]() 与
与![]() 在
在![]() 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数![]() 与
与![]() ,现给定区间
,现给定区间![]() .
.
(1)若![]() ,判断
,判断![]() 与
与![]() 是否在给定区间上接近;
是否在给定区间上接近;
(2)是否存在![]() ,使得
,使得![]() 与
与![]() 在给定区间
在给定区间![]() 上是接近的;若存在,求
上是接近的;若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,矩形![]() 和矩形
和矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 与平面
与平面![]() 及平面
及平面![]() 所成的角分别为
所成的角分别为![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,且
的中点,且![]() .
.
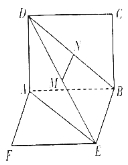
(1)求证:![]() 平面
平面![]() ;
;
(2)求线段![]() 的长;
的长;
(3)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,一个长轴端点为![]() ,离心率
,离心率![]() ,过P分别作斜率为
,过P分别作斜率为![]() 的直线PA,PB,交椭圆于点A,B。
的直线PA,PB,交椭圆于点A,B。
(1)求椭圆的方程;
(2)若![]() ,则直线AB是否经过某一定点?
,则直线AB是否经过某一定点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=![]() AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
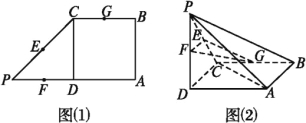
(1)求证:AP∥平面EFG;
(2)求三棱锥P-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=![]() ,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为
,且当规定主视图方向垂直平面ABCD时,该几何体的侧视图的面积为![]() .若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.
.若M、N分别是线段DE、CE上的动点,则AM+MN+NB的最小值为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的为( )
A. 线性相关系数r越大,两个变量的线性相关性越强
B. 线性相关系数r越小,两个变量的线性相关性越弱
C. 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D. 残差平方和越小的模型,模型拟合的效果越好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com