Question

【题目】直三棱柱ABC－A1B1C1中，AB＝AA1，∠CAB＝.

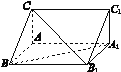
(1)证明：CB1⊥BA1；

(2)已知AB＝2，BC＝，求三棱锥C1－ABA1的体积．

Answer 1

【答案】（1）证明详见解析；（2）

【解析】试题分析：（1）连结AB1，则AC⊥BA1.，又∵AB＝AA1，∴四边形ABB1A1是正方形，∴BA1⊥AB1，由直线与平面垂直的判定定理可的BA1⊥平面CAB1，故CB1⊥BA1.（2）首先求出A1C1的值，由(1)知，A1C1⊥平面ABA1，即A1C1是三棱锥C1－ABA1的高，然后在求出△ABA1的面积，最后根据棱锥的体积公式求解即可.

试题解析：解：(1)证明：如图，连结AB1，

∵ABC－A1B1C1是直三棱柱，∠CAB＝，

∴AC⊥平面ABB1A1，故AC⊥BA1. 3分

又∵AB＝AA1，∴四边形ABB1A1是正方形，

∴BA1⊥AB1，又CA∩AB1＝A.

∴BA1⊥平面CAB1，故CB1⊥BA1. 6分

(2)∵AB＝AA1＝2，BC＝，∴AC＝A1C1＝1， 8分

由(1)知，A1C1⊥平面ABA1， 10分

∴VC1－ABA1＝S△ABA1·A1C1＝×2×1＝. 12分