
【题目】过点![]() 作曲线
作曲线![]() (其中
(其中![]() 为自然对数的底数)的切线,切点为
为自然对数的底数)的切线,切点为![]() ,设
,设![]() 在
在![]() 轴上的投影是点
轴上的投影是点![]() ,过点
,过点![]() 再作曲线
再作曲线![]() 的切线,切点为
的切线,切点为![]() ,设
,设![]() 在
在![]() 轴上的投影是点
轴上的投影是点![]() ,依次下去,得到第
,依次下去,得到第![]() 个切点
个切点![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
【答案】![]()
【解析】
设T1(x1,![]() ),可得切线方程代入点P坐标,可解得x1=0,即T1(0,1),可得H1(0,0),再写切线方程代入点H1(0,0),可得T2(1,e),H2(1,0),…
),可得切线方程代入点P坐标,可解得x1=0,即T1(0,1),可得H1(0,0),再写切线方程代入点H1(0,0),可得T2(1,e),H2(1,0),…
由此可推得规律,从而可得![]() 的坐标.
的坐标.
设T1(x1,![]() ),此处的导数为
),此处的导数为![]() ,
,
故切线方程为y﹣![]() =
=![]() (x﹣x1),代入点P(﹣1,0)
(x﹣x1),代入点P(﹣1,0)
可得0﹣![]() =
=![]() (﹣1﹣x1),解得x1=0,即T1(0,1),H1(0,0),
(﹣1﹣x1),解得x1=0,即T1(0,1),H1(0,0),
同理可得过点H1再作曲线C的切线方程为y﹣![]() =
=![]() (x﹣x2),代入点H1(0,0),
(x﹣x2),代入点H1(0,0),
可得0﹣![]() =
=![]() (0﹣x2),可解得x2=1,故T2(1,e),H2(1,0),
(0﹣x2),可解得x2=1,故T2(1,e),H2(1,0),
…
依次下去,可得Tn+1的坐标为(n,en),即得![]() =
=![]()
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣ax+(3﹣a)lnx,a∈R.
x2﹣ax+(3﹣a)lnx,a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线2x﹣y+1=0垂直,求a的值;
(2)设f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证:﹣5﹣f(x1)<f(x2)<﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说“如果物理成绩好,那么学习数学就没什么问题”某班针对“高中生物理对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如表:
编号 | 1 | 2 | 3 | 4 | 5 |
物理(x) | 90 | 85 | 74 | 68 | 63 |
数学(y) | 130 | 125 | 110 | 95 | 90 |
(参考公式:b= 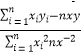 ,
, ![]() =
= ![]() b
b ![]() ,)参考数据:902+852+742+682+632=29394
,)参考数据:902+852+742+682+632=29394
90×130+85×125+74×110+68×95+63×90=42595.
(1)求数学y成绩关于物理成绩x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() (b精确到0.1),若某位学生的物理成绩为80分时,预测他的物理成绩.
(b精确到0.1),若某位学生的物理成绩为80分时,预测他的物理成绩.
(2)要从抽取的这五位学生中随机选出三位参加一项知识竞赛,以X表示选中的学生的数学成绩高于100分的人数,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P为正方体ABCD﹣A1B1C1D1中AC1与BD1的交点,则△PAC在该正方体各个面上的射影可能是( ) 
A.①②③④
B.①③
C.①④
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com