
分析 若所得函数为偶函数,则$\frac{π}{3}$-2φ=$\frac{π}{2}$+kπ,k∈Z,进而可得答案.
解答 解:把函数f(x)=3sin(2x+$\frac{π}{3}$)的图象向右平移φ个单位,
可得函数y=3sin[2(x-φ)+$\frac{π}{3}$]=3sin(2x+$\frac{π}{3}$-2φ)的图象,
若所得函数为偶函数,
则$\frac{π}{3}$-2φ=$\frac{π}{2}$+kπ,k∈Z,
解得:φ=-$\frac{π}{12}$+$\frac{1}{2}$kπ,k∈Z,
当k=1时,φ的最小正值为$\frac{5π}{12}$.
故答案为:$\frac{5π}{12}$.
点评 本题考查的知识点是正弦型函数的图象和性质,函数图象的平移变换,难度中档.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
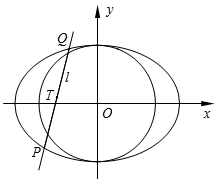 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
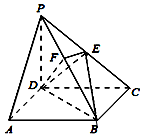 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,EF⊥PB交PB于点F.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
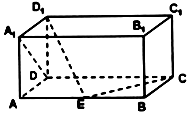 如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.
如上图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是90°,若D1E⊥EC,则直线A1D与平面D1DE所成的角为30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com