
(12分) 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且MD=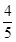 PD.
PD.
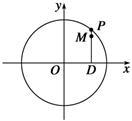
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为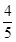 的直线被C所截线段的长度.
的直线被C所截线段的长度.
(1) 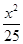 +
+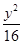 =1.(2)AB=
=1.(2)AB= .
.
【解析】
试题分析:设M的坐标为(x,y),P的坐标为(xP,yP),然后利用MD=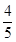 PD,把P点坐标用M点的坐标表示出来,代入圆的方程即可得到动点M的轨迹方程.
PD,把P点坐标用M点的坐标表示出来,代入圆的方程即可得到动点M的轨迹方程.
(1)设M的坐标为(x,y),P的坐标为(xP,yP),
由已知得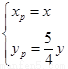 ∵P在圆上,
∵P在圆上,
∴x2+(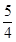 y)2=25,
y)2=25,
即轨迹C的方程为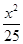 +
+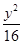 =1.
=1.
(2)过点(3,0)且斜率为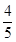 的直线方程为y=
的直线方程为y=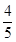 (x-3),
(x-3),
设直线与C的交点为A(x1,y1),B(x2,y2),将直线方程y=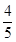 (x-3)代入C的方程,
(x-3)代入C的方程,
得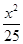 +
+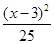 =1,即x2-3x-8=0.
=1,即x2-3x-8=0.
∴x1=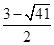 ,x2=
,x2=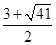 .
.
∴线段AB的长度为
AB=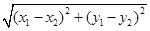
=
=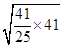 =
= .
.
考点:求轨迹方程,圆和椭圆的方程,直线与椭圆的位置关系,两曲线的交点.
点评:本小题属于相关点法求轨迹方程要把主动点的坐标用被动点的坐标表示出来,然后再代入主动点所在曲线的方程即可求出动点的轨迹方程.在涉及直线与椭圆相交求弦长时要借助韦达定理及弦长公式,一般不考虑求交点坐标.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011届重庆市万州二中高三下学期第一次月考考试数学理卷 题型:解答题
(本小题满分12分)
如图,设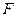 是椭圆
是椭圆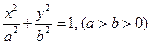 的左焦点,直线
的左焦点,直线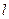 为对应的准线,直线
为对应的准线,直线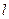 与
与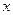 轴交于
轴交于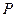 点,
点,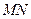 为椭圆的长轴,已知
为椭圆的长轴,已知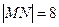 ,且
,且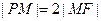 .
.
(1)求椭圆的标准方程;
(2)求证:对于任意的割线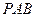 ,恒有
,恒有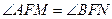 ;
;
(3)求三角形△ABF面积的最大值.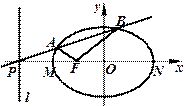
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省漳州市三校高三第二次联考文科数学 题型:解答题
(本小题满分12分)如图,设P是圆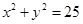 上的动点,点D是P在x轴上的
上的动点,点D是P在x轴上的
摄影,M为PD上一点,且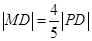
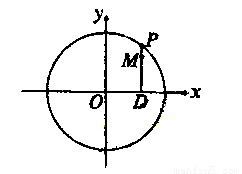
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为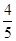 的直线被C所截线段的长度
的直线被C所截线段的长度
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省高三上学期11月月考文科数学 题型:解答题
(本小题满分12分)
如图,设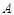 是单位圆和
是单位圆和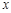 轴正半轴的交点,
轴正半轴的交点,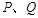 是单位圆上的两点,
是单位圆上的两点,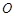 是
是
坐标原点,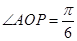 ,
,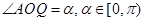 .
.
(1)若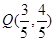 ,求
,求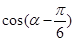 的值;
的值;
(2)设函数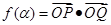 ,求
,求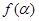 的值域.
的值域.

查看答案和解析>>
科目:高中数学 来源:2013届福建省高二上学期期中考试理科数学试卷 题型:解答题
(本小题满分12分)如图,设P是圆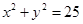 上的动点,点D是P在x轴上的射影,M为PD上一点,且
上的动点,点D是P在x轴上的射影,M为PD上一点,且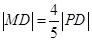
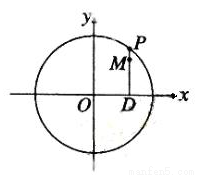
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为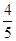 的直线被轨迹C所截线段的长度。
的直线被轨迹C所截线段的长度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com