
【题目】已知函数![]() .
.
(I)若曲线![]() 存在斜率为-1的切线,求实数a的取值范围;
存在斜率为-1的切线,求实数a的取值范围;
(II)求![]() 的单调区间;
的单调区间;
(III)设函数![]() ,求证:当
,求证:当![]() 时,
时, ![]() 在
在![]() 上存在极小值.
上存在极小值.
【答案】(Ⅰ) ![]() .(Ⅱ)答案见解析;(Ⅲ)证明见解析.
.(Ⅱ)答案见解析;(Ⅲ)证明见解析.
【解析】试题分析:
(1)求出函数的导数,问题转化为![]() 存在大于
存在大于![]() 的实数根,根据
的实数根,根据![]() 在
在![]() 时递增,求出
时递增,求出![]() 的范围即可;
的范围即可;
(2)求出函数的导数,通过讨论![]() 的范围,判断导数的符号,求出函数的单调区间即可;
的范围,判断导数的符号,求出函数的单调区间即可;
(3)求出函数![]() ,根据
,根据![]() ,得到存在
,得到存在![]() ,满足
,满足![]() ,从而让得到函数单调区间,求出函数的极小值,证处结论即可.
,从而让得到函数单调区间,求出函数的极小值,证处结论即可.
试题解析:
(I)由![]() 得
得![]() .
.
由已知曲线![]() 存在斜率为-1的切线,所以
存在斜率为-1的切线,所以![]() 存在大于零的实数根,
存在大于零的实数根,
即![]() 存在大于零的实数根,因为
存在大于零的实数根,因为![]() 在
在![]() 时单调递增,
时单调递增,
所以实数a的取值范围![]() .
.
(II)由![]() 可得
可得
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 的增区间为
的增区间为![]() ;
;
当![]() 时,若
时,若![]() ,
, ![]() ,若
,若![]() ,
, ![]() ,
,
所以此时函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(III)由![]() 及题设得
及题设得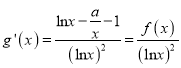 ,
,
由![]() 可得
可得![]() ,由(II)可知函数
,由(II)可知函数![]() 在
在![]() 上递增,
上递增,
所以![]() ,取
,取![]() ,显然
,显然![]() ,
,
![]() ,所以存在
,所以存在![]() 满足
满足![]() ,即存在
,即存在![]() 满足
满足![]() ,所以
,所以![]() ,
, ![]() 在区间(1,+∞)上的情况如下:
在区间(1,+∞)上的情况如下:
![]()
![]()
![]()
![]()
![]() - 0 +
- 0 +
![]() ↘ 极小 ↗
↘ 极小 ↗
所以当-1<a<0时,g(x)在(1,+∞)上存在极小值.


科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() )时,每小时的油耗(所需要的汽油量)为
)时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以![]() 千米/小时的速度行驶时,每小时的油耗为
千米/小时的速度行驶时,每小时的油耗为![]() 升,欲使每小时的油耗不超过
升,欲使每小时的油耗不超过![]() 升,求
升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶![]() 千米的油耗的最小值.
千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
(1)已知在全体样本中随机抽取![]() 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为![]() ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取![]() 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取![]() 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 在[0,7]上有1和6两个零点,且函数
在[0,7]上有1和6两个零点,且函数![]() 与函数
与函数![]() 都是偶函数,则
都是偶函数,则![]() 在[0,2019]上的零点至少有( )个
在[0,2019]上的零点至少有( )个
A.404B.406C.808D.812
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两动圆![]() 和
和![]() (
(![]() ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线![]() ,若曲线
,若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 满足:
满足:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)证明直线![]() 恒经过一定点,并求此定点的坐标;
恒经过一定点,并求此定点的坐标;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点至少有一个在原点右侧.
轴的交点至少有一个在原点右侧.
(1)求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,求
,求![]() 的值(其中
的值(其中![]() 表示不超过
表示不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() );
);
(3)对(2)中的![]() 求函数
求函数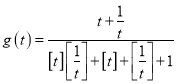 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为![]() (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com