
【题目】已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 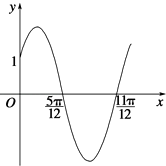
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间.
)的单调递增区间.
【答案】
(1)解:由图可知 ![]() ,可得T=π,
,可得T=π,
则 ![]() ,则ω=2,
,则ω=2,
又图象经过( ![]() ,0),
,0),
故有2× ![]() +φ=kπ,k∈Z,得φ=﹣
+φ=kπ,k∈Z,得φ=﹣ ![]() +kπ,
+kπ,
又0<φ< ![]() ,取φ=
,取φ= ![]() .
.
过(0,1)点,
所以Asinφ=1,可得A=2.
得f(x)=2sin(2x+ ![]() ).
).
(2)解:g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )=2sin[2(x﹣
)=2sin[2(x﹣ ![]() )+
)+ ![]() ]﹣2sin[2(x+
]﹣2sin[2(x+ ![]() )+
)+ ![]() ]
]
=2sin2x﹣2sin(2x+ ![]() )=2sin2x﹣2sin2xcos
)=2sin2x﹣2sin2xcos ![]() ﹣2cos2xsin
﹣2cos2xsin ![]() =sin2x﹣
=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() ),
),
由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
所以g(x)的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z.
],k∈Z.
【解析】(1)根据三角函数图象确定A,ω和φ的值即可求函数f(x)的解析式;(2)化简g(x),然后根据三角函数的单调性进行求解即可


科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an}和{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一期间,某商场决定从![]() 种服装、
种服装、![]() 种家电、
种家电、![]() 种日用品中,选出
种日用品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(1)试求选出![]() 种商品中至少有一种是家电的概率;
种商品中至少有一种是家电的概率;
(2)商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高![]() 元,规定购买该商品的顾客有
元,规定购买该商品的顾客有![]() 次抽奖的机会: 若中一次奖,则获得数额为
次抽奖的机会: 若中一次奖,则获得数额为![]() 元的奖金;若中两次奖,则获得数额为
元的奖金;若中两次奖,则获得数额为![]() 元的奖金;若中三次奖,则共获得数额为
元的奖金;若中三次奖,则共获得数额为 ![]() 元的奖金. 假设顾客每次抽奖中奖的概率都是
元的奖金. 假设顾客每次抽奖中奖的概率都是![]() ,请问: 商场将奖金数额
,请问: 商场将奖金数额![]() 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中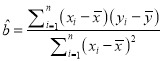 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
![]()
(1)画出茎叶图
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com