
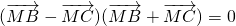 ,
,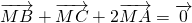 ,则△ABC的形状为
,则△ABC的形状为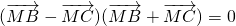 算出△MBC中MB=MC,△MBC是等腰三角形.而
算出△MBC中MB=MC,△MBC是等腰三角形.而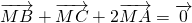 ,得到
,得到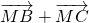 =-2
=-2 ,代入第一个等式可得
,代入第一个等式可得 •
•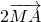 =0,从而得到BC⊥AM.再根据△MBC是等腰三角形,得到AM是BC的垂直平分线,可得AB=AC,而且M不是△ABC的重心,可得△ABC是等腰三角形且不是等边三角形,得到本题答案.
=0,从而得到BC⊥AM.再根据△MBC是等腰三角形,得到AM是BC的垂直平分线,可得AB=AC,而且M不是△ABC的重心,可得△ABC是等腰三角形且不是等边三角形,得到本题答案. 解:∵
解:∵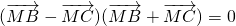
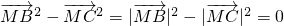 ,可得|
,可得| |=|
|=| |
|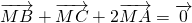 ,可得
,可得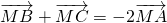
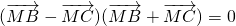 ,得
,得 •
•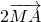 =0
=0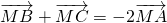 ,∴△ABC不是等边三角形
,∴△ABC不是等边三角形

科目:高中数学 来源: 题型:
| MB |
| MC |
| MB |
| MC |
| MA) |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MB |
| MC |
| MB |
| MC |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| MB |
| MC |
| MB |
| MC |
| A.正三角形 | B.直角三角形 |
| C.等腰三角形 | D.等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省绍兴一中高三(上)段考数学试卷(文科)(解析版) 题型:选择题
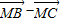 )•
)•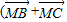 -2
-2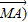 =0,则△ABC的形状为( )
=0,则△ABC的形状为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com