[题目]已知函数f=﹣f时.f(x)=2x . 则f(log280)= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数f（x）满足f（x+1）=﹣f（x﹣1），且当x∈（0，2）时，f（x）=2x ，则f（log280）= ．

【答案】
【解析】解：由f（x）满足f（x+1）=﹣f（x﹣1），

可得：f（x+1+1）=﹣f（x+1﹣1），即f（x+2）=﹣f（x）．

∴f（x+2+2）=﹣f（x+2），即f（x+4）=f（x）．

∴f（x）是周期函数，周期T=4．

由f（log280）=f（4+log25）=f（log25）．

当x∈（0，2）时，f（x）=2x，

那么：x﹣2∈（0，2）时，可得x∈（2，4），则f（x﹣2）=﹣f（x）．

即f（x）=﹣f（x﹣2）=﹣2x﹣2，

∵2＜log25＜4．

∴f（log25）= = ．

故f（log280）= ．

所以答案是：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】秦九韶是我国南宋时期的数学家，他在《数学九章》中提出的多项式的秦九韶算法，至今仍是比较先进的算法，如图是事项该算法的程序框图，执行该程序框图，若输入n，x的值分别为4，2，则输出v的值为（）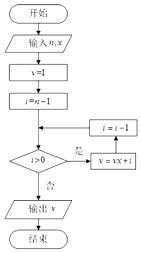
A.5
B.12
C.25
D.50

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】执行如图的程序框图，若程序运行中输出的一组数是（x，﹣12），则x的值为（　　）

A.27
B.81
C.243
D.729

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ax（lnx﹣1）（a≠0）．
（1）求函数y=f（x）的单调递增区间；
（2）当a＞0时，设函数g（x）= x3﹣f（x），函数h（x）=g′（x），
①若h（x）≥0恒成立，求实数a的取值范围；
②证明：ln（1×2×3×…×n）2e＜12+22+32+…+n2（n∈N*）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数为奇函数．
（1）求a的值；
（2）判断函数f（x）的单调性，并根据函数单调性的定义证明．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某油库的设计容量是30万吨，年初储量为10万吨，从年初起计划每月购进石油m万吨，以满足区域内和区域外的需求，若区域内每月用石油1万吨，区域外前x个月的需求量y（万吨）与x的函数关系为y= （p＞0，1≤x≤16，x∈N*），并且前4个月，区域外的需求量为20万吨．
（1）试写出第x个月石油调出后，油库内储油量M（万吨）与x的函数关系式；
（2）要使16个月内每月按计划购进石油之后，油库总能满足区域内和区域外的需求，且每月石油调出后，油库的石油剩余量不超过油库的容量，试确定m的取值范围．