

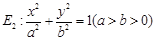 .
.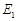 与
与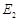 有相同的离心率,过点
有相同的离心率,过点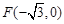 的直线
的直线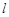 与
与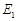 ,
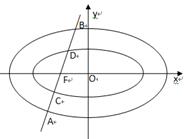
,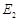 依次交于A,C,D,B四点(如图).当直线
依次交于A,C,D,B四点(如图).当直线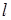 过
过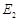 的上顶点时, 直线
的上顶点时, 直线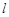 的倾斜角为
的倾斜角为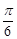 .
.
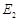 的方程;
的方程; 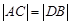 ;
; 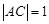 ,求直线
,求直线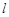 的方程.
的方程.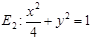 .(2)见解析;(3)
.(2)见解析;(3)
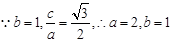 ,因此椭圆
,因此椭圆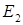 的方程为
的方程为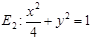 .
.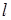 垂直
垂直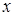 轴时,易求得
轴时,易求得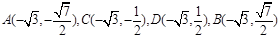
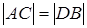 ,
,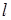 不垂直
不垂直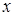 轴时,设
轴时,设
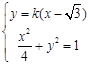
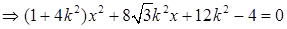 ①,
①,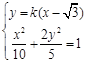
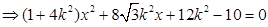 ②,
②, ,则
,则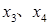 是方程①的解,
是方程①的解, 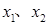 是方程②的解.
是方程②的解. ,
, 线段AB,CD的中点重合,
线段AB,CD的中点重合,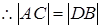
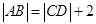 ,当直线
,当直线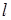 垂直
垂直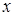 轴时,不合要求;
轴时,不合要求;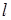 不垂直
不垂直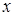 轴时,设
轴时,设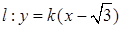 ,由(2)知,
,由(2)知,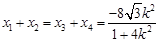 ,
,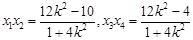 ,
,
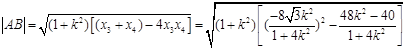
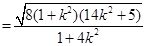
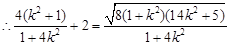 ,化简可得:
,化简可得:
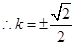 ,
,


 全优点练单元计划系列答案
全优点练单元计划系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com