
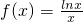 的图象为曲线C,函数
的图象为曲线C,函数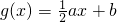 的图象为直线l.
的图象为直线l.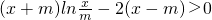
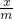 -2(x-m),x∈(m,+∞),
-2(x-m),x∈(m,+∞),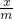 -2(x-m)>0,
-2(x-m)>0,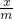 -2(x-m)>H(m),
-2(x-m)>H(m),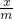 +
+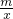 -1,
-1,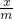 +
+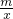 -1,G′(x)=
-1,G′(x)= -
-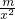 ,
, >0得,x>m,
>0得,x>m,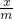 -2(x-m)>0,
-2(x-m)>0, a(x1+x2)+b]>2,
a(x1+x2)+b]>2, a
a +bx2-(
+bx2-( a
a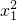 +bx1)]>2(x2-x1),
+bx1)]>2(x2-x1),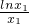 =
= ax1+b,
ax1+b,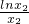 =
= ax2+b,
ax2+b, >2(x2-x1)(*),
>2(x2-x1)(*),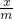 -2(x-m),x∈(m,+∞),通过导数法可研究出H(x)在x∈(m,+∞)单调递增,而H(m)=0,从而可使结论得证;
-2(x-m),x∈(m,+∞),通过导数法可研究出H(x)在x∈(m,+∞)单调递增,而H(m)=0,从而可使结论得证; a(x1+x2)+b]>2,只需证(x1+x2)[
a(x1+x2)+b]>2,只需证(x1+x2)[ a
a +bx2-(
+bx2-( a
a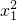 +bx1)]>2(x2-x1),结合(Ⅰ)的结论即可使问题解决.
+bx1)]>2(x2-x1),结合(Ⅰ)的结论即可使问题解决.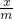 -2(x-m),x∈(m,+∞)是关键,探讨H(x)在x∈(m,+∞)单调递增是难点,突出考查分析法证题的作用,属于难题.
-2(x-m),x∈(m,+∞)是关键,探讨H(x)在x∈(m,+∞)单调递增是难点,突出考查分析法证题的作用,属于难题. 

科目:高中数学 来源: 题型:
(08年惠州一中五模理) 已知函数![]() 的图象为曲线E.
的图象为曲线E.
(Ⅰ) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(Ⅱ) 说明函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;
(Ⅲ) 在满足(2)的条件下,![]() 在
在![]() 恒成立,求c的取值范围.
恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() 的图象为曲线
的图象为曲线![]() ,函数
,函数![]()
![]() 的图象为曲线
的图象为曲线![]() .
.
(Ⅰ)若曲线![]() 和
和![]() 没有公共点,求实数
没有公共点,求实数![]() 的取值范围;
的取值范围;
(II)若![]() ,证明:当
,证明:当![]() 时,恒有
时,恒有![]() 成立;w.w.w.k.s.5.u.c.o.m
成立;w.w.w.k.s.5.u.c.o.m
(III)证明:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省高三9月月考理科数学 题型:解答题
21.(本小题满分12分)
已知函数 的图象为曲线
的图象为曲线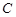 , 函数
, 函数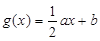 的图象为直线
的图象为直线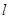 .
.
(Ⅰ) 当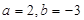 时, 求
时, 求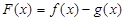 的最大值;
的最大值;
(Ⅱ) 设直线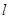 与曲线
与曲线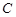 的交点的横坐标分别为
的交点的横坐标分别为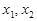 , 且
, 且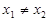 ,
,
求证: 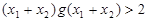 .
.
查看答案和解析>>
科目:高中数学 来源:2013届新疆乌鲁木齐八中高二上学期期末考试文科数学 题型:解答题
已知函数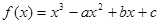 的图象为曲线C。
的图象为曲线C。
(1)若曲线C上存在点P,使曲线C在P点处的切线与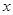 轴平行,求
轴平行,求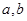 的关系;
的关系;
(2)若函数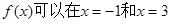 时取得极值,求此时
时取得极值,求此时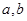 的值;
的值;
(3)在满足(2)的条件下,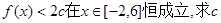 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com