
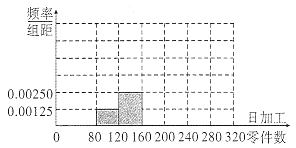
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,并统计他们的日加工零件数,得到以下数据;

(1)已知日加工零件数在![]() 范围内的5名员工中,有3名男工,2名女工,现从中任取两名进行指导,求他们性别不同的概率;
范围内的5名员工中,有3名男工,2名女工,现从中任取两名进行指导,求他们性别不同的概率;
(2)完成频率分布直方图,并估计全体新员工每天加工零件数的平均数(每组数据以中点值代替);
科目:高中数学 来源: 题型:
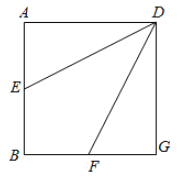
【题目】如图,棱长为![]() 的正方形
的正方形![]() 中,点
中,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,将
,将![]() ,
,![]() 沿
沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 两点重合于
两点重合于![]() 点上,设
点上,设![]() 与
与![]() 交于
交于![]() 点,过点
点,过点![]() 作
作![]() 于
于![]() 点.
点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(1)求椭圆的方程;
(2)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求证:直线
,求证:直线![]() 的斜率与直线MN的斜率之积为定值.
的斜率与直线MN的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面CDEF,且四边形ABCD是梯形,四边形CDEF是矩形,![]()
![]() ,M是线段DE上的点,满足DM=2ME.
,M是线段DE上的点,满足DM=2ME.
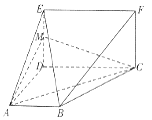
(1)证明:BE//平面MAC;
(2)求直线BF与平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是
是![]() 上的一个动点.当
上的一个动点.当![]() 是
是![]() 的上顶点时,
的上顶点时,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设斜率存在的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .若存在点
.若存在点![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
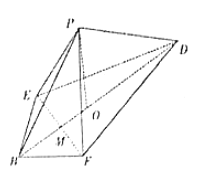
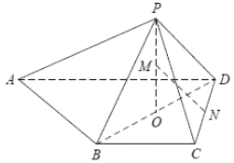
【题目】已知四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在底面
在底面![]() 上的射影是
上的射影是![]() 的中点
的中点![]() ,
,![]() .
.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)当四棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶然都不相邻的七位数有几个?
(答题要求:先列式,后计算 , 结果用具体数字表示.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com