
分析 2sin2x-5sin2y=1,可得:cos2x=$\frac{1-5si{n}^{2}y}{2}$≥0,解得$-\frac{\sqrt{5}}{5}$≤siny≤$\frac{\sqrt{5}}{5}$.cos2x+siny=$-\frac{5}{2}$$(siny-\frac{1}{5})^{2}$+$\frac{3}{5}$,再利用二次函数的单调性即可得出.
解答 解:∵2sin2x-5sin2y=1,
∴2(1-cos2x)-5sin2y=1,
解得cos2x=$\frac{1-5si{n}^{2}y}{2}$≥0,解得0≤sin2y$≤\frac{1}{5}$,∴$-\frac{\sqrt{5}}{5}$≤siny≤$\frac{\sqrt{5}}{5}$.
∴cos2x+siny
=$\frac{1-5si{n}^{2}y}{2}$+siny
=$-\frac{5}{2}$$(siny-\frac{1}{5})^{2}$+$\frac{3}{5}$,
∵$-\frac{\sqrt{5}}{5}$≤siny≤$\frac{\sqrt{5}}{5}$,
当siny=$\frac{1}{5}$时,cos2x+siny取得最大值$\frac{3}{5}$.
当siny=-$\frac{\sqrt{5}}{5}$时,cos2x+siny取得最小值$-\frac{\sqrt{5}}{5}$.
∴cos2x+siny∈$[-\frac{\sqrt{5}}{5},\frac{3}{5}]$,
故答案为:$[-\frac{\sqrt{5}}{5},\frac{3}{5}]$.
点评 本题考查了三角函数的单调性与值域、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\sqrt{2}$,一条准线方程为x=$\frac{\sqrt{2}}{2}$,直线l与双曲线右支及双曲线的渐近线交于A、B、C、D四点,四个点的顺序如图所示.
已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\sqrt{2}$,一条准线方程为x=$\frac{\sqrt{2}}{2}$,直线l与双曲线右支及双曲线的渐近线交于A、B、C、D四点,四个点的顺序如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 广告费用x(万元) | 3 | 4 | 5 | 6 |
| 年销售量t(件) | 25 | 30 | 40 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{70}}{5}$ | B. | $\frac{3\sqrt{70}}{5}$ | C. | $\frac{4\sqrt{15}}{5}$ | D. | $\frac{6\sqrt{15}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
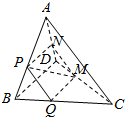 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )| A. | AC⊥BD | B. | AC∥截面PQMN | ||
| C. | AC=BD | D. | 异面直线PM与BD所成的角为45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com