练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，直线的参数方程为（为参数，），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求直线的普通方程与曲线的直角坐标方程；

    （2）若直线与曲线交于、两点，求的最小值.

    【答案】（1），；（2）

    【解析】分析：（1）将参数方程利用代入法消去参数可得直线的普通方程，利用 即可得曲线的直角坐标方程；（2）先证明直线过定点，点在圆的内部.当直线与线段垂直时，取得最小值，利用勾股定理可得结果..

    详解：（1）将（为参数，）消去参数，

    得直线，，即.

    将代入，得，

    即曲线的直角坐标方程为.

    （2）设直线的普通方程为，其中，又，

    ∴，则直线过定点，

    ∵圆的圆心，半径，，

    故点在圆的内部.

    当直线与线段垂直时，取得最小值，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某地每单位面积菜地年平均使用氮肥量x(单位:kg)与每单位面积蔬菜年平均产量Y(单位:t)之间的关系有如下数据:

    年份

    2000

    2001

    2002

    2003

    2004

    2005

    2006

    2007

    x/kg

    70

    74

    80

    78

    85

    92

    90

    95

    Y/t

    5.1

    6.0

    6.8

    7.8

    9.0

    10.2

    10.0

    12.0

    年份

    2008

    2009

    2010

    2011

    2012

    2013

    2014

    x/kg

    92

    108

    115

    123

    130

    138

    145

    Y/t

    11.5

    11.0

    11.8

    12.2

    12.5

    12.8

    13.0

    (1)求x与Y之间的相关系数,并检验是否线性相关;

    (2)若线性相关,求每单位面积蔬菜年平均产量Y与每单位面积菜地年平均使用氮肥量x之间的回归直线方程,并估计每单位面积菜地年平均使用氮肥150 kg时,每单位面积蔬菜的年平均产量.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为的函数（常数，为自然对数的底数）.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若恒成立，求实数的最大整数值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】
    （1）（坐标系与参数方程选做题）曲线C的直角坐标方程为x2+y2﹣2x=0，以原点为极点，x轴的正半轴为极轴建立积坐标系，则曲线C的极坐标方程为 ．
    （2）（不等式选做题）在实数范围内，不等式|2x﹣1|+|2x+1|≤6的解集为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，已知AB=AC=AA1= ，BC=4，点A1在底面ABC的投影是线段BC的中点O．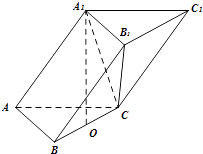

    （1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
    （2）求平面A1B1C与平面BB1C1C夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场销售价与上市时间的关系用图（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图（2）的抛物线段表示.

    （1）写出图（1）表示的市场售价与时间的函数关系式写出图（2）表示的种植成本与时间的函数关系式

    （2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？（注：市场售价和种植成本的单位：元/kg，时间单位：天.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，已知 ．
    （1）求证：tanB=3tanA；
    （2）若cosC= ，求A的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均为正数的两个数列{an}和{bn}满足：an+1= ，n∈N* ，
    （1）设bn+1=1+ ，n∈N*，求证：数列{ }是等差数列；
    （2）设bn+1= ，n∈N*，且{an}是等比数列，求a1和b1的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}前三项的和为﹣3，前三项的积为8．
    （1）求等差数列{an}的通项公式；
    （2）若a2 ， a3 ， a1成等比数列，求数列{|an|}的前n项和．

    查看答案和解析>>

    同步练习册答案