
分析 $\frac{\sqrt{1+\sqrt{x}}+\sqrt{1-\sqrt{x}}}{\sqrt{1+\sqrt{x}}-\sqrt{1-\sqrt{x}}}$可化为:$\sqrt{\frac{1}{x}}$-$\sqrt{\frac{1}{x}-1}$,将x=$\frac{1}{8-4\sqrt{3}}$代入再将被开方数化为完全平方式,脱去根号,可得答案.
解答 解:$\frac{\sqrt{1+\sqrt{x}}+\sqrt{1-\sqrt{x}}}{\sqrt{1+\sqrt{x}}-\sqrt{1-\sqrt{x}}}$=$\frac{(\sqrt{1+\sqrt{x}}+\sqrt{1-\sqrt{x}})^{2}}{(\sqrt{1+\sqrt{x}}-\sqrt{1-\sqrt{x}})(\sqrt{1+\sqrt{x}}+\sqrt{1-\sqrt{x}})}$=$\frac{(1+\sqrt{x})+(1-\sqrt{x})+2\sqrt{1-x}}{(1+\sqrt{x})-(1-\sqrt{x})}$=$\frac{1+\sqrt{1-x}}{\sqrt{x}}$=$\sqrt{\frac{1}{x}}$+$\sqrt{\frac{1}{x}-1}$,
当x=$\frac{1}{8-4\sqrt{3}}$时,原式=$\sqrt{8-4\sqrt{3}}$+$\sqrt{7-4\sqrt{3}}$=$\sqrt{(\sqrt{6}-\sqrt{2})^{2}}$+$\sqrt{{(2-\sqrt{3})}^{2}}$=$\sqrt{6}-\sqrt{2}+2-\sqrt{3}$,
故答案为:$\sqrt{6}-\sqrt{2}+2-\sqrt{3}$
点评 本题考查的知识点是指数式的化简与求值,本题解答时技巧性较强,否则运算起来非常麻烦.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
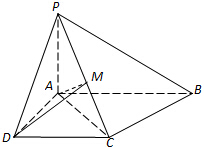 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:2 | B. | 2:3 | C. | 3:7 | D. | 7:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com