
【题目】汽车的普及给人们的出行带来了诸多方便,但汽车超速行驶也造成了诸多隐患.为了解某一段公路汽车通过时的车速情况,现随机抽测了通过这段公路的200辆汽车的时速,所得数据均在区间![]() 中,其频率分布直方图如图所示.
中,其频率分布直方图如图所示.
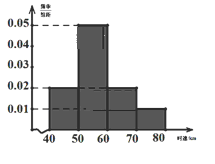
(1)求被抽测的200辆汽车的平均时速.
(2)该路段路况良好,但属于事故高发路段,交警部门对此路段过往车辆限速![]() .对于超速行驶,交警部门对超速车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.罚款情况如下:
.对于超速行驶,交警部门对超速车辆有相应处罚:记分(扣除驾驶员驾照的分数)和罚款.罚款情况如下:
超速情况 | 10%以内 | 10%~20% | 20%~50% | 50%以上 |
罚款情况 | 0元 | 100元 | 150元 | 可以并处吊销驾照 |
①求被抽测的200辆汽车中超速在10%~20%的车辆数.
②该路段车流量比较大,按以前统计该路段每天来往车辆约2000辆.试预估每天的罚款总数.
【答案】(1) ![]() (2) ① 20辆;②44000辆
(2) ① 20辆;②44000辆
【解析】
(1)根据频率分布直方图的平均数的计算公式计算;(2)①首先计算超速在10%~20%的速度在![]() 之间,根据频率分布直方图可求得这个区间的面积,即频率,
之间,根据频率分布直方图可求得这个区间的面积,即频率,![]() 频率=频数,即超速在10%~20%的车辆数;②根据①可知罚款100元的频率
频率=频数,即超速在10%~20%的车辆数;②根据①可知罚款100元的频率![]() ,速度在
,速度在![]() 之间的频率
之间的频率![]() ,最后罚款总额为
,最后罚款总额为![]() .
.
(1)平均时速![]()
(2)①超速在10%~20%的速度在![]() 之间
之间
速度在![]() 之间的车辆数为
之间的车辆数为![]() 辆
辆
速度在![]() 之间的车辆数为
之间的车辆数为![]() 辆
辆
速度在![]() 之间的车辆数为
之间的车辆数为![]() 辆
辆
所以速度在![]() 之间的车辆数为
之间的车辆数为![]() 辆
辆
故超速10%~20%的车辆约![]() 辆
辆
②设任意一辆车的罚款数为![]() ,被抽测的200辆汽车中均没有超速50%以上,
,被抽测的200辆汽车中均没有超速50%以上,
故![]() 元
元
所以预计罚款总数约为![]() 元
元


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,有下列四个命题:
,有下列四个命题:
①若![]() 是奇函数,则
是奇函数,则![]() 的图象关于点
的图象关于点![]() 对称;
对称;
②若对![]() ,有
,有![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③若对![]() ,有
,有![]() ,则
,则![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
其中正确命题的序号为__________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 上存在两点
上存在两点![]() ,椭圆
,椭圆![]() 上存在两个
上存在两个![]() 点满足:
点满足:![]() 三点共线,
三点共线,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() 两个品牌的共享单车在编号分别为
两个品牌的共享单车在编号分别为![]() 的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市 品牌 | 1 | 2 | 3 | 4 | 5 |
A品牌 | 3 | 4 | 12 | 6 | 8 |
B品牌 | 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有85%的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对A品牌要从这五个城市选择三个城市进行宣传,
(ⅰ)求城市2被选中的概率;
(ⅱ)求在城市2被选中的条件下城市3也被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两班本次考试数学分数如下列茎叶图所示:
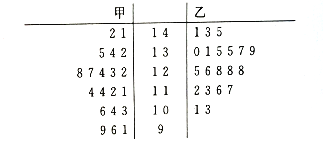
(I)根据基叶图求甲、乙两班同学数学分数的中位数,并将乙班同学的分数的频率分布直方图填充完整;
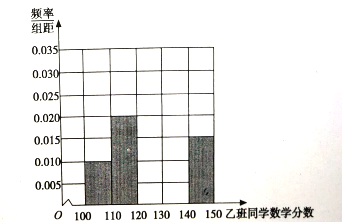
(Ⅱ)根据基叶图比较在一模考试中,甲、乙两班同学数学分数的平均水平和分数的分散程度(不要求计算出具体值,给出结论即可)
(Ⅲ)若规定分数在![]() 的成绩为良好,分数在
的成绩为良好,分数在![]() 的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出12位同学参加数学提优培训,求这12位同学中恰含甲、乙两班所有140分以上的同学的概率.
的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出12位同学参加数学提优培训,求这12位同学中恰含甲、乙两班所有140分以上的同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A'B'C'D'棱长为2,并且E,F分别是棱AA',CC'的中点.

(Ⅰ)求证:平面BED'F⊥平面BB'D'D;
(Ⅱ)求直线A'B'与平面BED'F所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com