
【题目】已知抛物线C:y2=2px(p>0),过其焦点F的直线l交抛物线C于点A、B,|AF|=3|BF|,则|AB|=( )
A.p
B.![]()
C.2p
D.![]()
【答案】D
【解析】解:设抛物线y2=2px(p>0)的准线为l′:x=﹣ ![]() . 如图所示,
. 如图所示,
①当直线AB的倾斜角为锐角时,
分别过点A,B作AM⊥l′,BN⊥l′,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵|AF|=3|BF|= ![]() |AB|,
|AB|,
∴|AM|﹣|BN|=|AC|=|AF|﹣|BF|= ![]() |AB|,
|AB|,
在Rt△ABC中,由|AC|= ![]() |AB|,可得∠BAC=60°.
|AB|,可得∠BAC=60°.
∵AM∥x轴,∴∠BAC=∠AFx=60°.
∴kAB=tan60°= ![]() ,
,
直线方程为y= ![]() (x﹣
(x﹣ ![]() ),代入抛物线方程,可得3x2﹣5px+
),代入抛物线方程,可得3x2﹣5px+ ![]() p2=0,
p2=0,
∴|AB|= ![]() =
= ![]() p,
p,
②当直线AB的倾斜角为钝角时,可得kAB=﹣ ![]() .|AB|=
.|AB|= ![]() p
p
综上可知:|AB|= ![]() p,
p,
故选:D.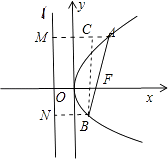


科目:高中数学 来源: 题型:
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图: 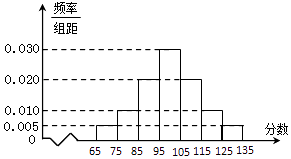
(1)求这部分学生成绩的样本平均数 ![]() 和样本方差s2(同一组数据用该组的中点值作为代表)
和样本方差s2(同一组数据用该组的中点值作为代表)
(2)由频率分布直方图可以认为,该校高二学生在这次测验中的数学成绩X服从正态分布 ![]() . ①利用正态分布,求P(X≥129);
. ①利用正态分布,求P(X≥129);
②若该校高二共有1000名学生,试利用①的结果估计这次测验中,数学成绩在129分以上(含129分)的学生人数.(结果用整数表示)
附:① ![]() ≈14.5②若X~N(μ,σ2),则P(μ﹣2σ<X<μ+2σ)=0.9544.
≈14.5②若X~N(μ,σ2),则P(μ﹣2σ<X<μ+2σ)=0.9544.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),满足f(x+1)=f(x﹣1),且f(x)在[﹣3,﹣2]上是增函数,又α、β是锐角三角形的两个内角,则( )
A.f(sinα)>f(cosβ)
B.f(cosα)<f(cosβ)
C.f(sinα)<f(cosβ)
D.f(sinα)<f(sinβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:方程 ![]() =1表示焦点在x轴上的椭圆,q:双曲线
=1表示焦点在x轴上的椭圆,q:双曲线 ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() ).
).
(1)若椭圆 ![]() =1的焦点和双曲线
=1的焦点和双曲线 ![]() =1的顶点重合,求实数m的值;
=1的顶点重合,求实数m的值;
(2)若“p∧q”是真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )上单调,则ω的最大值为( )
)上单调,则ω的最大值为( )
A.11
B.9
C.7
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com