
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
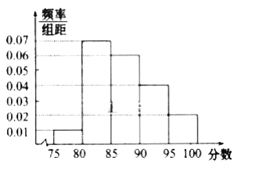
![]() 分别求第
分别求第![]() 组的频率;
组的频率;
![]() 若该校决定在第
若该校决定在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名学生进入第二轮面试,
名学生进入第二轮面试,
![]() 已知学生甲和学生乙的成绩均在第
已知学生甲和学生乙的成绩均在第![]() 组,求学生甲和学生乙同时进入第二轮面试的概率;
组,求学生甲和学生乙同时进入第二轮面试的概率;
![]() 根据直方图试估计这
根据直方图试估计这![]() 名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法中
①.对于命题![]() :存在
:存在![]() ,则
,则![]() :
:![]() ;
;
②.命题“若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数”的逆命题为假命题;
上是增函数”的逆命题为假命题;
③.若![]() 为真命题,则
为真命题,则![]() 均为真命题;
均为真命题;
④.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”.
”.
错误的是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.回归直线过样本点的中心![]() .
.
B.对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
C.两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D.在回归直线方程![]() =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求△
,求△![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com