
| 商店名称 | A | B | C | D | E |
| 销售额x/千万 | 3 | 5 | 6 | 7 | 9 |
| 利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
分析 (1)根据所给的这组数据,写出利用最小二乘法要用的量的结果,把所求的这些结果代入公式求出线性回归方程的系数,进而求出a的值,写出线性回归方程.
(2)根据上一问做出的线性回归方程,把x=4的值代入方程,估计出对应的y的值.
解答 解:(1)由题中的数据可知$\overline{x}$=6,$\overline{y}$=3.4.
所以b=$\frac{-3×(-1.4)+(-1)×(-0.4)+1×0.6+3×1.6}{9+1+1+9}$=$\frac{1}{2}$.
a=3.4-$\frac{1}{2}×6$=0.4.
所以利润额y关于销售额x的回归直线方程为y=0.5x+0.4.
(2)由(1)知,当x=4时,y=0.5×4+0.4=2.4,
所以当销售额为4(千万元)时,可以估计该店的利润额为2.4(百万元).
点评 本题考查线性回归方程的求法和应用,是一个基础题,这种题目解题的关键是求出最小二乘法所要用到的量,数字的运算不要出错.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{2}{3}π$) | B. | ($\frac{π}{6}$,$\frac{5}{6}π$) | C. | [$\frac{π}{3}$,$\frac{5}{6}π$) | D. | ($\frac{5}{6}π$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
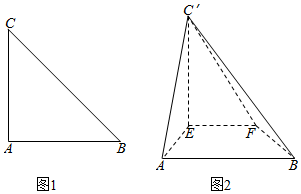 如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′-ABFE
如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′-ABFE查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊥n | B. | m∥n | C. | m与n相交 | D. | m与n异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充分必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 为偶函数 | B. | 为奇函数 | ||
| C. | 既为奇函数又为偶函数 | D. | 为非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com