
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
【答案】(1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB平面ABD,AB⊥BD,
∴AB⊥平面BCD,又CD平面BCD,∴AB⊥CD.
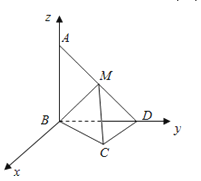
(2)解:建立如图所示的空间直角坐标系.
∵AB=BD=CD=1,AB⊥BD,CD⊥BD,
∴B(0,0,0),C(1,1,0),A(0,0,1),D(0,1,0),M![]() .
.
∴![]() =(0,1,﹣1),
=(0,1,﹣1),![]() =(1,1,0),
=(1,1,0),![]() =
=![]() .
.
设平面BCM的法向量![]() =(x,y,z),则
=(x,y,z),则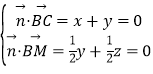 ,
,
令y=﹣1,则x=1,z=1.
∴![]() =(1,﹣1,1).
=(1,﹣1,1).
设直线AD与平面MBC所成角为θ.
则sinθ=|cos<![]() ,
,![]() >|=
>|=![]() =
=![]() =
=![]() .
.
【解析】(1)利用面面垂直的性质定理即可得出;
(2)建立如图所示的空间直角坐标系.设直线AD与平面MBC所成角为θ,利用线面角的计算公式sinθ=|cos<![]() ,
,![]() >|=
>|=![]() 即可得出.
即可得出.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判断f(x)的奇偶性并证明;
(II)若m=![]() ,判断f(x)在(3,+∞)的单调性(不用证明);
,判断f(x)在(3,+∞)的单调性(不用证明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)]?若存在,求出此时m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:①定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,则
,则![]() 一定不是
一定不是![]() 上的减函数;
上的减函数;
②用反证法证明命题“若实数![]() ,满足
,满足![]() ,则
,则![]() 都为0”时,“假设命题的结论不成立”的叙述是“假设
都为0”时,“假设命题的结论不成立”的叙述是“假设![]() 都不为0”;
都不为0”;
③把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得到的图象的函数解析式为
个单位长度,所得到的图象的函数解析式为![]() ;
;
④“![]() ”是“函数
”是“函数![]() 为奇函数”的充分不必要条件.
为奇函数”的充分不必要条件.
其中所有正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是海面上一条南北方向的海防警戒线,在
是海面上一条南北方向的海防警戒线,在 ![]() 上点
上点 ![]() 处有一个水声监测点,另两个监测点
处有一个水声监测点,另两个监测点 ![]() 分别在
分别在 ![]() 的正东方向
的正东方向 ![]() 处和
处和 ![]() 处.某时刻,监测点
处.某时刻,监测点 ![]() 收到发自目标
收到发自目标 ![]() 的一个声波,
的一个声波,![]() 后监测点
后监测点 ![]() 后监测点
后监测点 ![]() 相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是
相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是 ![]() .
.

(1)设 ![]() 到
到 ![]() 的距离为
的距离为 ![]() ,用
,用 ![]() 分别表示
分别表示 ![]() 到
到 ![]() 的距离,并求
的距离,并求 ![]() 的值;
的值;
(2)求目标 ![]() 的海防警戒线
的海防警戒线 ![]() 的距离(精确到
的距离(精确到 ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E:![]() ﹣
﹣![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: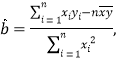
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com