【答案】
分析:(1)根据条件,写出函数F(x)=f(x)-g(x),利用配方法可知F(x)在[3,+∞)上单调递增,从而可求函数的值域;
(2)写出G(x)=x
3+x
2-10x+8,再用定义法证明即可;
(3)利用图象法求解,由f(x)=g(x)得x|x-a|+4=x+2即x|x-a|=x-2,构造两个函数,在同一坐标系中,作出它们的图象,从而得解.
解答:解(1)F(x)=f(x)-g(x)=x
2-4x-2=(x-2)
2-6--------------------------(3分)
F(x)在[3,+∞)上单调递增,------------------------(4分)
当x∈[3,+∞)时,F(x)的值域为[-5,+∞)-------------------------------------------------(6分)
(2)G(x)=f(x)•g(x)=(x
2-3x+2)(x+4)=x
3+x
2-10x+8---------------------------------------(8分)
对任意x
1,x
2∈[3,+∞),且x
1<x
2由G(x
1)-G(x
2)=(x
1-x
2)(x
12+x
1x
2+x
22+x
1+x
2-10)<0
知G(x)=f(x)•g(x)在[3,+∞)上的单调递增.-----------------------------------------(12分)
(3)由f(x)=g(x)得x|x-a|+4=x+2即x|x-a|=x-2
令

,p(x)=x-2--------------------(14分)
由图象容易得到
当a=0时,两图象只有一个交点,不合题意;
当a<0时,由x
2-(a+1)x+2=0,令
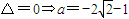
所以,当
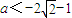
时,符合题意----------------------------------(16分)
当a>0时,令p(x)=x-2=0⇒x=2,所以要使得两图象有三个交点,必须a>2,
所以当

或a>2时,方程f(x)=g(x)有三个不同的解;----------------------(18分)
 点评:
点评:本题的考点是函数与方程的综合运用,主要考查函数的单调性,函数的值域,考查方程解的研究,关键是合理构造函数,合理转化.

 ,p(x)=x-2--------------------(14分)
,p(x)=x-2--------------------(14分)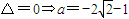
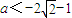 时,符合题意----------------------------------(16分)
时,符合题意----------------------------------(16分) 或a>2时,方程f(x)=g(x)有三个不同的解;----------------------(18分)
或a>2时,方程f(x)=g(x)有三个不同的解;----------------------(18分)


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案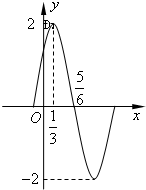 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<