
【题目】已知![]() 是两条不重合的直线,
是两条不重合的直线, ![]() 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若![]() ,
, ![]() ,则
,则![]() ;
;
②若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
③若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
④当![]() ,且
,且![]() 时,若
时,若![]() ,则
,则![]() .
.
其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为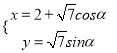 (其中
(其中![]() 为参数),曲线
为参数),曲线![]() :
: ![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
, ![]() 分别交于
分别交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋中放有形状大小相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个,从袋中随机抽取一个小球,取到标号为2的小球的概率为
个,从袋中随机抽取一个小球,取到标号为2的小球的概率为![]() ,现从袋中不放回地随机取出2个小球,记第一次取出的小球标号为
,现从袋中不放回地随机取出2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1)记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(2)在区间![]() 上任取两个实数
上任取两个实数![]() ,求事件
,求事件![]() “
“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“鸡兔同笼”问题是我国古代著名的趣题之一.《孙子算经》中就记载了这个有趣的问题.书中这样描述:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔几何?
试设计一个算法,输入鸡兔的总数量和鸡兔的脚的总数量,分别输出鸡、兔的数量,写出程序语句.并画出相应的程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆![]() 的周长和面积同时等分成两部分的函数称为圆
的周长和面积同时等分成两部分的函数称为圆![]() 的一个“太极函数”.下列有关说法中:
的一个“太极函数”.下列有关说法中:

①对圆![]() 的所有非常数函数的太极函数中,一定不能为偶函数;
的所有非常数函数的太极函数中,一定不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的太极函数;
的太极函数;
④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数.
的太极函数.
所有正确说法的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com