
已知函数 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求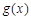 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
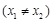 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
(1)极大值为1,无极小值;(2)3-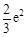 ;(3)
;(3)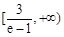 .
.
解析试题分析:(1)求
科目:高中数学
来源:
题型:解答题
设
科目:高中数学
来源:
题型:解答题
已知
科目:高中数学
来源:
题型:解答题
设函数
科目:高中数学
来源:
题型:解答题
定义在定义域
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区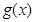 的极值,就是先求出
的极值,就是先求出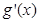 ,解方程
,解方程 ,此方程的解把函数的定义域分成若干个区间,我们再确定在每个区间里
,此方程的解把函数的定义域分成若干个区间,我们再确定在每个区间里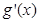 的符号,从而得出极大值或极小值;(2)此总是首先是对不等式
的符号,从而得出极大值或极小值;(2)此总是首先是对不等式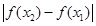
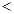
 恒成立的转化,由(1)可确定
恒成立的转化,由(1)可确定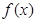 在
在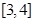 上是增函数,同样的方法(导数法)可确定函数
上是增函数,同样的方法(导数法)可确定函数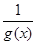 在
在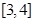 上也是增函数,不妨设
上也是增函数,不妨设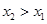 ,这样题设绝对值不等式可变为
,这样题设绝对值不等式可变为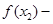
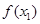
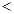
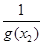
 ,整理为
,整理为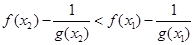 ,由此函数
,由此函数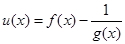 在区间
在区间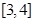 上为减函数,则
上为减函数,则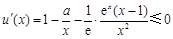 在(3,4)上恒成立,要求
在(3,4)上恒成立,要求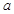 的取值范围.采取分离参数法得
的取值范围.采取分离参数法得 恒成立,于是问题转化为求
恒成立,于是问题转化为求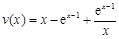 在
在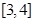 上的最大值;(3)由于
上的最大值;(3)由于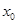 的任意性,我们可先求出
的任意性,我们可先求出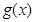 在
在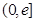 上的值域
上的值域 ,题设“在区间
,题设“在区间 上总存在
上总存在 ,使得
,使得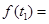
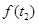
 成立”,转化为函数
成立”,转化为函数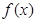 在区间
在区间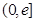 上不是单调函数,极值点为
上不是单调函数,极值点为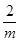 (
( ),其次
),其次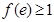 ,极小值
,极小值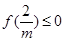 ,最后还要证明在
,最后还要证明在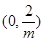 上,存在
上,存在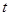 ,使
,使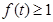 ,由此可求出
,由此可求出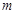 的范围.
的范围.
试题解析:(1)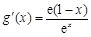 ,令
,令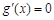 ,得x=1. 1分
,得x=1. 1分
列表如下:x (-∞,1) 1 (1,+∞) 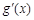
+ 0 - g(x) ↗ 

湘岳假期暑假作业系列答案
快乐暑假假日乐园小升初系列答案
赢在起跑线快乐暑假河北少年儿童出版社系列答案
名校联盟金考卷期末大冲刺系列答案
暑假生活湖南少年儿童出版社系列答案
暑假小小练系列答案
暑假作业新世界出版社系列答案
创新成功学习快乐暑假云南科技出版社系列答案
暑假生活安徽教育出版社系列答案
假期生活智趣暑假系列答案
 ,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值. (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.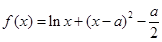 ,
,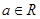 .
.
(1)若函数 在
在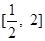 上单调递增,求实数
上单调递增,求实数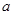 的取值范围;
的取值范围;
(2)求函数 的极值点.
的极值点.
(3)设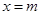 为函数
为函数 的极小值点,
的极小值点,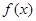 的图象与
的图象与 轴交于
轴交于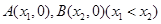 两点,且
两点,且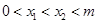 ,
,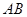 中点为
中点为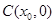 ,
,
求证: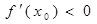 .
.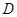 内的函数
内的函数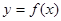 ,若对任意的
,若对任意的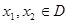 都有
都有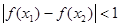 ,则称函数
,则称函数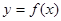 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数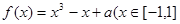 ,(
,(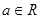 )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号