
【题目】已知某手机品牌公司的年固定成本为40万元,每生产1万部手机还需要另投入16万元,设该公句一年内生产x万部并全部销售完,每1万部手机的销售收入为![]() 万元,且
万元,且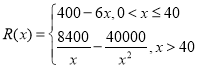 .
.
(1)写出年利润(万元)关于年产量![]() (万部)的函数解析式;
(万部)的函数解析式;
(2)当年产量多少万部时,公司在该款手机生产获得最大利润,并求出最大利润.
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足;对任意
,如果满足;对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若![]() 是
是![]() 上的有界函数,且
上的有界函数,且![]() 的上界为3,求实数
的上界为3,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求函数
,求函数![]() 在
在![]() 上的上界
上的上界![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则称
,p为常数),则称![]() 为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
A.![]() 不是等方差数列;
不是等方差数列;
B.若![]() 既是等方差数列,又是等差数列,则该数列为常数列;
既是等方差数列,又是等差数列,则该数列为常数列;
C.已知数列![]() 是等方差数列,则数列
是等方差数列,则数列![]() 是等方差数列;
是等方差数列;
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列.
,k为常数)也是等方差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
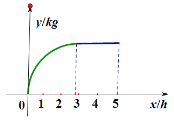
A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00-99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
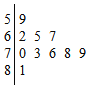
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩的茎叶图如图所示,这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和
和![]() ,过抛物线
,过抛物线![]() 上一点
上一点![]() 作两条直线与
作两条直线与![]() 分别相切于
分别相切于![]() 两点,分别交抛物线于
两点,分别交抛物线于![]() 两点.
两点.

(1)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率;
的斜率;
(2)若直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有1998名运动员号码为1~1998这1998个自然数,从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com