
 ,有如下四个结论:
,有如下四个结论: 是等边三角形;③
是等边三角形;③ 与
与 所成的角为
所成的角为 ;④
;④ 与平面
与平面 成
成 的角。
的角。 .
.
 与
与 所成的角为
所成的角为 ;根据向量的夹角公式得到成立,而
;根据向量的夹角公式得到成立,而 与平面
与平面 成
成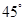 的角。故填写①②③
的角。故填写①②③

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源:不详 题型:解答题
 的底面是菱形,且
的底面是菱形,且 面
面 ,
, ,
, ,
, 为棱
为棱 的中点,
的中点, 为线段
为线段 的中点,
的中点,
 面
面 ;
; 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; 的体积.
的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
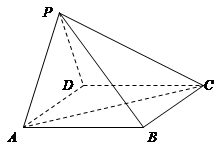
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
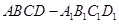 的棱线长为1,面对角线
的棱线长为1,面对角线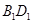 上有两个动点E,F,且
上有两个动点E,F,且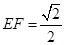 ,则下列四个结论中①
,则下列四个结论中①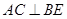 ②
②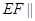 平面
平面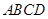 ③三棱锥
③三棱锥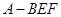 的体积为定值 ④异面直线
的体积为定值 ④异面直线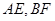 所成的角为定值,其中正确的个数是
所成的角为定值,其中正确的个数是| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,AB=2CD=8.
,AB=2CD=8.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球 |
| B.一个等腰三角形绕着底边上的高所在直线旋转180º形成的封闭曲面所围成的图形叫做圆锥 |
| C.用平面去截圆锥,底面与截面之间的部分叫做圆台 |
| D.以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com