
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过点
的焦点重合,过点![]() 与
与![]() 的长轴垂直的直线交
的长轴垂直的直线交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 的标准方程;
的标准方程;
(2)若动直线![]() 与
与![]() 相切,且与
相切,且与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 的标准方程为
的标准方程为![]() .
.![]() 的标准方程为
的标准方程为![]() .(2)
.(2) ![]()
【解析】
(1)先由已知设抛物线![]() 的方程为
的方程为![]() ,根据抛物线
,根据抛物线![]() 过点
过点![]() ,即可求出抛物线方程,得出
,即可求出抛物线方程,得出![]() 坐标,再由题意可得
坐标,再由题意可得![]() ,进而可求出椭圆方程;又曲线
,进而可求出椭圆方程;又曲线![]() 是以坐标原点
是以坐标原点![]() 为圆心,以
为圆心,以![]() 为半径的圆,根据
为半径的圆,根据![]() 坐标坐标得出
坐标坐标得出![]() 的值,即可写出圆的标准方程;
的值,即可写出圆的标准方程;
(2)先由直线![]() 与
与![]() 相切,得圆心
相切,得圆心![]() 到直线
到直线![]() 的距离为1,因此
的距离为1,因此![]() ,根据题意分类讨论:当直线
,根据题意分类讨论:当直线![]() 的斜率不存在和斜率存在两种情况,结合韦达定理和弦长公式,分别求出
的斜率不存在和斜率存在两种情况,结合韦达定理和弦长公式,分别求出![]() 的范围即可.
的范围即可.
解:(1)由已知设抛物线![]() 的方程为
的方程为![]() ,
,
则![]() ,解得
,解得![]() ,即
,即![]() 的标准方程为
的标准方程为![]() .
.
则![]() ,不妨设椭圆
,不妨设椭圆![]() 的方程为
的方程为![]() ,
,
由 ,得
,得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() ,
,
故![]() 的标准方程为
的标准方程为![]() .
.
易知![]() ,所以
,所以![]() 的标准方程为
的标准方程为![]() .
.
(2)因为直线![]() 与
与![]() 相切,所以圆心
相切,所以圆心![]() 到直线
到直线![]() 的距离为1.所以
的距离为1.所以![]() .
.
当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,易知两种情况所得到的
,易知两种情况所得到的![]() 的面积相等.
的面积相等.
由 ,得
,得![]() .
.
不妨设![]() ,
,![]() ,则
,则![]() ,
,
此时![]() .
.
当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,
,
则![]() ,即
,即![]() .
.
由 ,得
,得![]() ,
,
所以![]()
![]() 恒成立.
恒成立.
设![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
所以 .
.
令![]() ,则
,则![]() ,
,
所以![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
易知![]() 区间
区间![]() 上单调递减,所以
上单调递减,所以![]() .
.
综上,![]() 的面积
的面积![]() 的取值范围为
的取值范围为![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】2018年12月1日,贵阳市地铁一号线全线开通,在一定程度上缓解了出行的拥堵状况.为了了解市民对地铁一号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图:
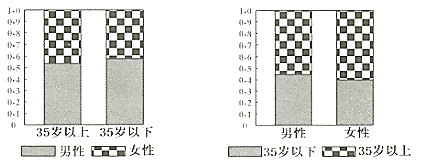
根据图中(![]() 岁以上含
岁以上含![]() 岁)的信息,下列结论中不一定正确的是( )
岁)的信息,下列结论中不一定正确的是( )
A. 样本中男性比女性更关注地铁一号线全线开通
B. 样本中多数女性是![]() 岁以上
岁以上
C. ![]() 岁以下的男性人数比
岁以下的男性人数比![]() 岁以上的女性人数多
岁以上的女性人数多
D. 样本中![]() 岁以上的人对地铁一号线的开通关注度更高
岁以上的人对地铁一号线的开通关注度更高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽奖活动中,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
(1)求![]() 能获一等奖的概率;
能获一等奖的概率;
(2)若![]() ,
,![]() 已获一等奖,求
已获一等奖,求![]() 能获奖的概率.
能获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,设函数
,设函数![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的两动点,且以
上的两动点,且以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点的凸四边形的面积的最大值为
四个点为顶点的凸四边形的面积的最大值为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若椭圆![]() 经过点
经过点![]() ,且直线
,且直线![]() 的斜率是直线
的斜率是直线![]() ,
,![]() 的斜率的等比中项,求
的斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() .
.
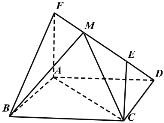
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)设平面![]() 与平面
与平面![]() 所成二面角的大小为
所成二面角的大小为![]() (
(![]() ),求
),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
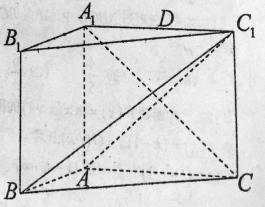
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是
是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求点
,若存在,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com