
【题目】如果定义在R上的函数f(x),对任意的x∈R,都有f(﹣x)≠﹣f(x),则称该函数是“β函数”.
(Ⅰ) 分别判断下列函数:①y=2x;②y=2x+1; ③y=x2﹣2x﹣3,是否为“β函数”?(直接写出结论)
(Ⅱ) 若函数f(x)=sinx+cosx+a是“β函数”,求实数a的取值范围;
(Ⅲ) 已知f(x)= ![]() 是“β函数”,且在R上单调递增,求所有可能的集合A与B.
是“β函数”,且在R上单调递增,求所有可能的集合A与B.
【答案】解:(Ⅰ)①、②是“β 函数”,③不是“β函数”.…(3分)
(Ⅱ)由题意,对任意的x∈R,f(﹣x)≠﹣f(x),即f(﹣x)+f(x)≠0,.
因为f(x)=sinx+cosx+a,所以f(﹣x)=﹣sinx+cosx+a.
故f(﹣x)+f(x)=2cosx+2a
由题意,对任意的x∈R,2cosx+2a≠0,即a≠﹣cosx
故实数a的取值范围为(﹣∞,﹣1)∪(1,+∞).
(Ⅲ)①对任意的x≠0
(a)若x∈A且﹣x∈A,则﹣x≠x,f(﹣x)=f(x),这与y=f(x)在R上单调递增矛盾,(舍),
(b)若x∈B且﹣x∈B,则f﹣(x)=﹣x=﹣f(x),这与y=f(x)是“β函数”矛盾,(舍).
此时,由y=f(x)的定义域为R,故对任意的x≠0,x与﹣x恰有一个属于A,另一个属于B.
②假设存在x0<0,使得x0∈A,则由x0< ![]() ,故f(x0)<f(
,故f(x0)<f( ![]() ).
).
(a)若 ![]() ,则f(
,则f( ![]() )=
)= ![]() ,矛盾,
,矛盾,
(b)若 ![]() ,则f(
,则f( ![]() )=
)= ![]() ,矛盾.
,矛盾.
综上,对任意的x<0,xA,故x∈B,即(﹣∞,0)B,则(0,+∞)A.
③假设0∈B,则f(﹣0)=﹣f(0)=0,矛盾.故0∈A
故A=[0,+∞),B=(﹣∞,0).
经检验A=[0,+∞),B=(﹣∞,0).符合题意
【解析】(Ⅰ)有题设可判断。(Ⅱ)根据题意代入“β函数”的形式可得到f(﹣x)+f(x)=2cosx+2a![]() 0,即a≠﹣cosx。(Ⅲ)由题意先判断集合A和集合B内元素的存在性。再假设存在x0<0,由反证法得到对任意的x<0,xA,故x∈B,即(﹣∞,0)B,则(0,+∞)A.这个结论。再讨论特殊点假设0∈B时矛盾得到0∈A即A=[0,+∞),B=(﹣∞,0).
0,即a≠﹣cosx。(Ⅲ)由题意先判断集合A和集合B内元素的存在性。再假设存在x0<0,由反证法得到对任意的x<0,xA,故x∈B,即(﹣∞,0)B,则(0,+∞)A.这个结论。再讨论特殊点假设0∈B时矛盾得到0∈A即A=[0,+∞),B=(﹣∞,0).


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点, 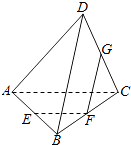
(1)求证:BD∥平面EFG;
(2)若AD=CD,AB=CB,求证:AC⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.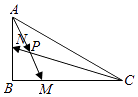
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,对于
,对于 ![]() 上的任意x1 , x2 , 有如下条件:
上的任意x1 , x2 , 有如下条件:
① ![]() ;②|x1|>x2;③x1>|x2|;④
;②|x1|>x2;③x1>|x2|;④ ![]() .
.
其中能使g(x1)>g(x2)恒成立的条件序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(x+1)的图象,只需把函数y=sinx的图象上所有的点( )
A.向左平行移动1个单位长度
B.向右平行移动1个单位长度
C.向左平行移动π个单位长度
D.向右平行移动π个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)
p(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 ![]() .
.
(Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)将函数y=f(x)的图象向右平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com