
【题目】设m,n∈R,若直线l:mx+ny﹣1=0与x轴相交于点A,与y轴相交于点B,且l与圆x2+y2=4相交所得弦的长为2,O为坐标原点,则△AOB面积的最小值为 .
【答案】3
【解析】解:由圆x2+y2=4的方程,得到圆心坐标为(0,0),半径r=2, ∵直线l与圆x2+y2=4相交所得弦CD=2,
∴圆心到直线l的距离d= 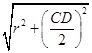 =
= ![]() ,
,
∴圆心到直线l:mx+ny﹣1=0的距离d= ![]() =
= ![]() ,
,
整理得:m2+n2= ![]() ,
,
令直线l解析式中y=0,解得:x= ![]() ,
,
∴A( ![]() ,0),即OA=
,0),即OA= ![]() ,
,
令x=0,解得:y= ![]() ,
,
∴B(0, ![]() ),即OB=
),即OB= ![]() ,
,
∵m2+n2≥2|mn|,当且仅当|m|=|n|时取等号,
∴|mn|≤ ![]() ,
,
又△AOB为直角三角形,
∴S△ABC= ![]() OAOB=
OAOB= ![]() ≥
≥ ![]() =3,当且仅当|m|2=|n|2=
=3,当且仅当|m|2=|n|2= ![]() 时取等号,
时取等号,
则△AOB面积的最小值为3.
所以答案是:3.
【考点精析】关于本题考查的一般式方程,需要了解直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0)才能得出正确答案.
(A,B不同时为0)才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F与椭圆C的一个焦点重合,且抛物线的准线与椭圆C相交于点 ![]() .
. 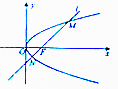
(1)求抛物线的方程;
(2)过点F是否存在直线l与椭圆C交于M,N两点,且以MN为对角线的正方形的第三个顶点恰在y轴上?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.
(1)求AC边所在直线方程;
(2)求顶点C的坐标;
(3)求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,点A(﹣2,0),B(2,0),C(x,1) (i)若∠ACB是直角,则x=
(ii)若△ABC是锐角三角形,则x的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( ) 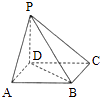
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=x|x﹣a|.
(1)当a=0时,写出函数y=f(x)的单调递增区间;
(2)当a=1时,讨论函数y=f(x)的奇偶性;
(3)设a≠0,函数y=f(x)在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围(用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.
(1)求函数f(x)(x∈R)的解析式;
(2)现已画出函数f(x)在y轴左侧的图象,如图所示,请补全完整函数f(x)的图象;
(3)求使f(x)>0的实数x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)已知方程x2+(m﹣3)x+m=0有两个不等正实根,求实数m的取值范围.
(2)不等式(m2﹣2m﹣3)x2﹣(m﹣3)x﹣1<0对任意x∈R恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com