分析:(1)连接A1C,由已知可判断△A1AC为正三角形,根据等边三角形三线合一结合平面A1ACC1⊥平面ABC,可得A1O⊥平面ABC,进而由线面垂直的定义,得到A1O⊥BC;
(2)连接MC,可证得四边形A1OCM为平行四边形,结合(1)的结论及线面垂直的第二判定定理可得MC⊥平面ABC,则∠MNC为直线MN与平面ABC所成的角,解三角形MNC可得答案.
解答:证明:(1)连接A
1C
∵A
1A=AC=2,∠A
1AC=60°,
∴△A
1AC为正三角形
又∵O为AC的中点
∴A
1O⊥AC
∵平面A
1ACC
1⊥平面ABC,且平面A
1ACC
1∩平面ABC=AC,A
1O?平面A
1ACC
1
∴A
1O⊥平面ABC,
∵BC?平面ABC
∴A
1O⊥BC
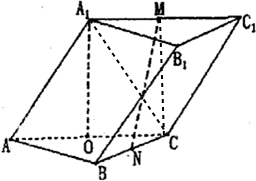
解:(2)连接MC
∵M,O分别是A
1C
1,AC的中点.
∴四边形A
1OCM为平行四边形
∵A
1O⊥平面ABC,A
1O∥MC
∴MC⊥平面ABC,且MC=A
1O
∴∠MNC为直线MN与平面ABC所成的角
由(1)得MC=
,NC=1
在Rt△MNC中,tan∠MNC=
=
∴∠MNC=60°
即直线MN与平面ABC所成的角为60°
点评:本题考查的知识点是直线与平面所成的角,直线与平面垂直的性质,其中熟练掌握空间线面垂直,线线垂直,面面垂直之间的相互转化关系是解答的关键.

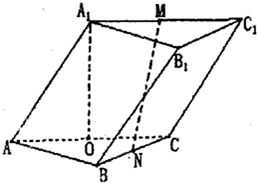 (2011•洛阳二模)如图,在三棱柱ABC-A1B1C1中,△ABC为正三角形,A1A=AC=2,∠A1AC=60°,平面A1ACC1⊥平面ABC,O为AC的中点.
(2011•洛阳二模)如图,在三棱柱ABC-A1B1C1中,△ABC为正三角形,A1A=AC=2,∠A1AC=60°,平面A1ACC1⊥平面ABC,O为AC的中点.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案