
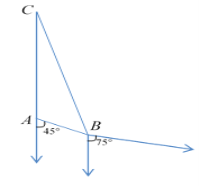
【题目】如图,在海岸A处,发现南偏东45°方向距A为(2![]() -2)海里的B处有一艘走私船,在A处正北方向,距A为
-2)海里的B处有一艘走私船,在A处正北方向,距A为![]() 海里的C处的缉私船立即奉命以10
海里的C处的缉私船立即奉命以10![]() 海里/时的速度追截走私船.
海里/时的速度追截走私船.
(1)刚发现走私船时,求两船的距离;
(2)若走私船正以10![]() 海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:
海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:![]() ≈1.4,
≈1.4,![]() ≈2.5).
≈2.5).
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
【题目】在边长为4的正方形ABCD的边上有动点P,动点P从B点开始沿折线BCDA运动到A终止,设P点移动的距离为x,![]() 的面积为S.
的面积为S.
(1)求函数S=f(x)的解析式、定义域,画出函数图像;
(2)求函数S=f(x)的值域. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(![]() )若圆心
)若圆心![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,求切线的方程.
的切线,求切线的方程.
(![]() )若圆
)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域是{x|x≠0},对定义域内的任意![]() ,
,![]() 都有f(
都有f(![]() ·
·![]() )=f(
)=f(![]() )+f(
)+f(![]() ),且当x>1时,f(x)>0,f(2)=1.
),且当x>1时,f(x)>0,f(2)=1.
(1)证明:![]() (x)是偶函数;
(x)是偶函数;
(2)证明:![]() (x)在(0,+∞)上是增函数;
(x)在(0,+∞)上是增函数;
(3)解不等式![]() (2
(2![]() -1)<2.
-1)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com