
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 在区间[1,2]上的最大值;
在区间[1,2]上的最大值;
(2)设![]() 在(0,2)内恰有两个极值点,求实数m的取值范围.
在(0,2)内恰有两个极值点,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)对函数求导,判断函数单调性,由单调性即可得到函数的最值;(2)先求出f′(x),由题意知:mx2﹣4x+m=0在(0,2)有两个变号零点,即![]() 在(0,2)有两个变号零点,构造函数,利用导数求出最值即可.
在(0,2)有两个变号零点,构造函数,利用导数求出最值即可.
(1)![]() ,∴p′(x)=ex﹣
,∴p′(x)=ex﹣![]() ,
,
∴p″(x)=ex+![]() >0恒成立
>0恒成立
所以p′(x)=ex﹣![]() 在[1,2]单调递增,
在[1,2]单调递增,
∵p'(1)=e﹣3<0,![]() ,∴x0∈(1,2),使p'(x0)=0,
,∴x0∈(1,2),使p'(x0)=0,
当x∈[1,x0]时,p'(x)<0,p(x)单调递减;
当x∈[x0,2]时,p'(x)>0,p(x)单调递增.
又![]() ,
,![]() >e+2
>e+2
∴p(x)在[1,2]上的最大值为p(2)=e2﹣3ln2+2.
(2)![]() ,
,![]() ,
,
由题意知:![]() =0在(0,2)有两个变号零点,
=0在(0,2)有两个变号零点,
即![]() 在(0,2)有两个变号零点
在(0,2)有两个变号零点
令![]() ,
,![]() ,
,
令![]() 则x=1,且
则x=1,且![]() 时,
时,![]() ,g(x)单调递增;
,g(x)单调递增;![]() 时,
时,![]() g(x)单调递减,
g(x)单调递减,
又g(0)=0,g(1)=2,g(2)=![]() ,
,
![]()
![]()


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线C相交于A,B两点,与圆
与抛物线C相交于A,B两点,与圆![]() 相交于D,E两点,O为坐标原点,
相交于D,E两点,O为坐标原点,![]() ,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬果经销商销售某种蔬果,售价为每公斤25元,成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价以每公斤10元处理完.根据以往的销售情况,得到如图所示的频率分布直方图:

(1)根据频率分布直方图计算该种蔬果日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了250公斤这种蔬果,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
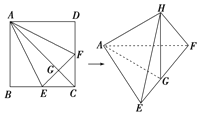
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且点
,且点![]() 与椭圆C的上顶点构成边长为2的等边三角形.
与椭圆C的上顶点构成边长为2的等边三角形.

(1)求椭圆C的方程;
(2)已知直线l与椭圆C相切于点P,且分别与直线![]() 和直线
和直线![]() 相交于点
相交于点![]() .试判断
.试判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com