
【题目】已知指数函数![]() =
= ![]() 满足
满足![]() 定义域为
定义域为![]() 的函数
的函数![]() =
=![]() 是奇函数.
是奇函数.
(1)确定函数![]() 与
与![]() 的解析式;
的解析式;
(2)若对任意的![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) g(x)=2x,f(x)= ![]() (2)k<
(2)k<![]() .
.
【解析】试题分析:(1)由指数函数y=g(x)=ax满足: ![]() 求出a的值,可得函数g(x)的解析式;f(x)=
求出a的值,可得函数g(x)的解析式;f(x)= ![]() ,再由奇函数求出m的值即可;
,再由奇函数求出m的值即可;
(2)由(1)知f(x)= ![]() ,易知f(x)在(﹣
,易知f(x)在(﹣![]() ,+
,+![]() )上为减函数,则原不等式等价于f(t2﹣2t)<﹣f(2t2﹣k)=f(k﹣2t2),等价于t2﹣2t>k﹣2t2, 对一切t∈R恒成立,由判别式
)上为减函数,则原不等式等价于f(t2﹣2t)<﹣f(2t2﹣k)=f(k﹣2t2),等价于t2﹣2t>k﹣2t2, 对一切t∈R恒成立,由判别式![]() <0可得结论.
<0可得结论.
试题解析:(1)∵指数函数y=g(x)=ax满足: ![]()
则a=2,
所以g(x)=2x,
所以f(x)= ![]() ,
,
因为它是奇函数.0是函数的定义域的值,
所以f(0)=0,即![]() ,
,
则n=1,
所以f(x)= ![]() ,
,
又由f(1)=﹣f(-1)知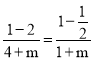 ,
,
所以m=2,
f(x)= ![]() .
.
(2)由(1)知f(x)= ![]() ,
,
易知f(x)在(﹣![]() ,+
,+![]() )上为减函数.
)上为减函数.
又因f(x)是奇函数,从而不等式:
f(t2﹣2t)+f(2t2﹣k)<0等价于f(t2﹣2t)<﹣f(2t2﹣k)=f(k﹣2t2),
因f(x)为减函数,由上式推得:t2﹣2t>k﹣2t2,
即对一切t∈R有:3t2﹣2t﹣k>0,
从而判别式![]() =4+12k<0,解得:k<
=4+12k<0,解得:k<![]() .
.
点晴:本题考查函数单调性函数奇偶性以及恒成立问题:本题首先利用函数f(x)的奇偶性将不等式f(t2﹣2t)+f(2t2﹣k)<0转化为f(t2﹣2t)<f(k﹣2t2),再利用f(x)的单调性推得:t2﹣2t>k﹣2t2,最后得到对一切t∈R有:3t2﹣2t﹣k>0,从而判别式![]() =4+12k<0,解得:k<
=4+12k<0,解得:k<![]() .
.


科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成如图所示的人体脂肪含量与年龄关系的散点图.根据该图,下列结论中正确的是( ) 
A.人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20%
B.人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20%
C.人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20%
D.人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是侧棱
是侧棱![]() 上的动点.
上的动点.
(1)求四棱锥![]() 的表面积;
的表面积;
(2)是否在棱![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ;若存在,指出点
;若存在,指出点![]() 的位置,并证明;若不存在,请说明理由.
的位置,并证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() 月)的关系
月)的关系![]() 有以下叙述:
有以下叙述:
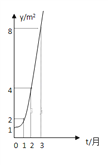
①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过![]()
③浮萍从![]() 蔓延到
蔓延到![]() 需要经过1.5个月;
需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到![]() 所经过的时间分别为
所经过的时间分别为![]() 则
则![]() .其中正确的是
.其中正确的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当
,当![]() 时,恒有
时,恒有![]() .当
.当![]() 时,
时, ![]() .
.
(Ⅰ)求证: ![]() 是奇函数;
是奇函数;
(Ⅱ)若![]() ,试求
,试求![]() 在区间
在区间![]() 上的最值;
上的最值;
(Ⅲ)是否存在![]() ,使
,使![]() 对于任意
对于任意![]() 恒成立?若存在,求出实数
恒成立?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近来景德镇市棚户区改造进行的如火如荼,加上城市人居环境的不断改善,我市房地产住宅销售价格节节攀升,一部分刚需住户带来了不小的烦恼,下表为我市2017.1﹣2017.5这5月住宅价格与月份的关系.
月份x | 1 | 2 | 3 | 4 | 5 |
住宅价格y | 4.8 | 5.4 | 6.2 | 6.6 | 7 |
(1)通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度(精确到0.01)
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系. ①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8![]() ,圆环的圆心
,圆环的圆心![]() 距离地面的高度为10
距离地面的高度为10![]() ,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点
,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点![]() 处.
处.
(1)试确定在时刻![]() (
(![]() )时蚂蚁距离地面的高度
)时蚂蚁距离地面的高度![]() ;
;
(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过14![]() ?
?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com